Postfiksna notacija - kako računari računaju?

Uvod

Uobičajeni način zapisivanja matematičkih izraza (koji podrazumeva da se znak operacije zapisuje između dva operanda), poznat je kao infiksna notacija i ima sledeće odlike:

znaci operacija povezuju operande (promenljive i brojčane vrednosti)
operacije množenja i deljenja imaju veći prioritet od operacija sabiranja i oduzimanja
zagrade imaju najveći prioritet i pojavljuju se po potrebi - zarad definisanja prioriteta različitih delova izraza

Shodno utvrđenim pravilima sa kojima se susrećemo kako u matematici tako i u svakodnevnom životu, do vrednosti izraza dolazi se na nedvosmislen način, što možemo ilustrovati preko izraza 5 * (2 + 4) u kome sabiranje prethodi množenju (s obzirom na to da se sabirci nalaze u zagradi), i stoga se izraz prvo svodi na 5 * 6, a potom na krajnji rezultat 30.

Međutim, iako je - iz perspektive ljudi - postupak računanja preko infiksne notacije: razumljiv, jednostavan za usvajanje i (reklo bi se) prijemčiv i neproblematičan, za upotrebu u računarskoj tehnici - infiksna notacija ni iz daleka nije najbolji izbor.

Možda ne deluje intuitivno na prvi pogled, ali, izrazi nalik na ab+ i ab+cd-/ koji su zapisani korišćenjem tzv. postfiksne notacije, na računarima se rešavaju primetno brže od odgovarajućih infiksnih izraza a+b i (a+b)/(c-d).

U nastavku ćemo ukratko prodiskutovati o tome zašto infiksna notacija nije optimalan izbor za računarske algoritme * koji se tiču računanja vrednosti izraza, nakon čega ćemo se pozabaviti "tehničkim osobinama" postfiksnog zapisa ....

Nedostaci infiksne notacije

.... u kontekstu primene u računarskim algoritmima

Iz perspektive programera koji tek savladavaju osnove i nisu se još uvek susretali sa metodama za procenu vrednosti algebarskih izraza, ideja o korišćenju uobičajene infiksne notacije u računarskim algoritmima - verovatno deluje "prirodno", ali, u implementaciji takve ideje, postoje problemi koji se (najprostije rečeno) svode na to da računari - za razliku od ljudi - nisu sposobni da odjednom sagledaju "širu sliku". *

Čak i u slučaju jednostavnog infiksnog izraza u formatu a * (b + c) (kao u uvodu), računarski program ne može sa sigurnošću izvršavati operacije u onom trenutku kada se pojave, to jest - u opštem smislu - potrebno je bar jednom proći kroz ceo izraz (u najboljem slučaju) - i tek onda je moguće vratiti se na izvršavanje operacija.

Zapravo, izraz ne mora obuhvatiti ni dve operacije: izraz u formatu a + b skoro je najjednostavniji mogući izraz, ali, ni u ovom slučaju računar ne sme odmah da obavi sabiranje (sve dok ne uzme u obzir sve operande i operatore).

Posmatrajući stvari u modernom kontekstu, mnogi čitaoci se mogu zapitati šta je toliko "strašno" u vezi sa tim da program prođe kroz izraz više puta, uzme u obzir sve operande, operatore, zagrade i .... "nekako" .... odredi prioritet izvršavanja operacija, jer, u današnje vreme, čak i slabiji procesori mogu sve navedeno izvršiti u deliću sekunde (ili - još jednostavnije - ne deluje da je postupak računanja preko infiksne notacije "posebno problematičan"), međutim:

kao programeri, u obavezi smo da uvek tražimo što bolja i što efikasnija rešenja (pogotovo kada su u pitanju elementarni problemi), čime ostavljamo što manje 'zbrke' generacijama programera koje dolaze posle nas
poslednje što smo naveli, posebno je važilo na početku razvoja računarske industrije, kada računari, ne samo da nisu bili veoma brzi, već su (naprotiv) bili prilično 'tromi' *

U praktičnom smislu, nedostatak brzine prvobitnih računara (čak i po pitanju jednostavnih operacija kao što je računanje vrednosti matematičkih izraza), bio je takav da je neko vreme dovodio u pitanje početak razvoja računarske industrije ** ("ako računari ne mogu efikasno rešavati jednostavne matematičke izraze, kako se onda mogu koristiti za komplikovanije zadatke?!"), ali, problem je rešio holandski naučnik Edzger Dajkstra i ostavio pokoljenjima lep, jednostavan i efikasan algoritam koji se zasniva na isto tako lepom, jednostavnom i efikasnom (ali 'ne baš' uobičajenom), načinu beleženja matematičkih izraza ....

Nekoliko usputnih napomena

* Sasvim je moguće napisati program koji će (naizgled) "osposobiti" računar da "sagleda širu sliku", ali, može se reći da je jedini iole praktičan način za realizaciju takvog programa - upotreba postupka koji će biti prikazan na kraju (u opštem smislu, pošto se kreira tzv. stablo izraza, prilično lako se može re-kreirati i bilo koji oblik notacije (preko stabla), i može se 'simulirati' direktno prepoznavanje prioriteta operacija unutar infiksnog izraza).

** Ukoliko želite da "postavite stvari u perspektivu", zamislite da je pokretanje jednostavnih programa za izračunavanje vrednosti izraza, na prvobitnim računarima, okvirno nalikovalo pokušaju da se na mobilnom telefonu sa početka 21. veka pokrene program za tabelarne proračune.

Teško je proceniti, iz sadašnje perspektive, da li smo dobro 'odmerili gornje poređenje', ali (u svakom slučaju), krajem pedesetih godina 20. veka, za pokretanje najosnovnijih programa bilo je potrebno više dana programiranja elektronskih sklopova, pojedinačne instrukcije izvršavale su se po nekoliko sekundi, i stoga je znatno efikasniji algoritam za računanje, bio - više nego dobrodošao!

*** Krajem 50-ih godina 20. veka postojali su računari (u veoma malom broju), ali, može se reći da računarska industrija - praktično nije postojala ("još uvek", i pogotovo ne u obimu sa kakvim se srećemo u današnje vreme).

Postfiksna notacija

Postfiksna notacija * je sistem za zapisivanje matematičkih izraza, sa sledećim glavnim odlikama:

operatori se pojavljuju posle operanada
zagrade se ne pojavljuju u izrazima

Sistem za zapisivanje izraza u postfiksnom obliku razradio je australijski naučnik Čarls Hamblin, sredinom pedesetih godina 20. veka, po ugledu na (idejno sličnu) prefiksnu notaciju, koju je izumeo poljski matematičar Jan Lukašijevič i objavio 1924. godine.

Na prvi pogled, zapisivanje izraza bez zagrada može delovati "čudno", ali, uz iole ozbiljnije udubljivanje, prednosti postaju prilično očigledne - pogotovo kad je u pitanju upotreba u računarskim sistemima. **

Oblik izraza u postfiksnoj notaciji

Kao što smo prethodno naveli, pojava znaka operacije posle operanada, najočiglednija je odlika postfiksne notacije, što možemo ilustrovati preko sledećih primera:

izraz a + b postaje ab+
izraz a + b * c postaje abc*+

Da bismo mogli razumeti pravi smisao ovakvog načina zapisivanja (to jest, da bismo mogli razumeti zašto postfiksni izrazi predstavljaju praktičniji način zapisa matematičkih izraza na računarima (u odnosu na infiksnu notaciju)), potrebno je sagledati kako se računa vrednost postfiksnih izraza, i potrebno je razmotriti kako postfiksni izrazi uopšte nastaju.

Postupak računanja vrednosti postfiksnog izraza pokazaćemo odmah (u nastavku), u daljem toku članka pokazaćemo na koji način ljudi mogu pretvarati infiksne izraze u postfiksne (sagledavanjem i rasuđivanjem), a uskoro ćemo nekoliko članaka posvetiti i nešto komplikovanijem algoritamskom postupku za pretvaranje infiksnih izraza u postfiksne izraze.

Pri računanju vrednosti izraza, smatraćemo da promenljive imaju sledeće vrednosti:

a = 4
b = 3
c = 2

.... iz čega sledi da vrednost izraza a * (b + c), odnosno, izraza 4 * (3 + 2), iznosi 20.

Kada se u postfiksnoj notaciji promenljive zamene navedenim (konkretnim) vrednostima, izraz postaje:

4 3 2 + *

Računanje vrednosti

Postfiksni izrazi rešavaju se na sledeći način:

posmatrajući elemente sleva nadesno, traži se prvi (ili, u opštem smislu - sledeći ), znak operacije
kada se pronađe znak operacije, nad dve vrednosti levo od znaka obavlja se operacija koja odgovara znaku
umesto dva operanda i znaka (iz prethodnog koraka), u izrazu ostaje samo rezultat operacije
postupak se ponavlja sve dok u izrazu ne ostane samo jedan operand (posle poslednje izvršene operacije)
preostali operand predstavlja vrednost početnog izraza

U primeru koji razmatramo (izraz: 4 3 2 + *), prvo se u obzir uzima znak operacije sabiranja, kome odgovaraju dve brojčane vrednosti sa leve strane, 3 i 2 (ili, praktično, prvo se rešava izraz 3 2 +):

obavlja se operacija sabiranja
rezultat sabiranja (5), ostaje u izrazu umesto brojeva 3 i 2
znak koji predstavlja operaciju sabiranja, uklanja se iz izraza

Izraz postaje: 4 5 * (na sličan način kako je izraz 4 * (3 + 2) mogao biti sveden na izraz 4 * 5), i preostaje samo da se postupak ponovi sa operacijom množenja - pri čemu se dobija rezultat 20.

Poenta je sledeća: ceo izraz (kao što vidimo), rešava se u jednom prolasku, to jest, svaka operacija obavlja se u onom trenutku kada se naiđe na znak operacije:

nema dvoumljenja (za ljude) *
relativno lako se može osmisliti i računarski algoritam ** koji funkcioniše po sličnom principu (bez grananja, tj. odlučivanja)

* Na početku smo naveli da je najočiglednija odlika postfiksne notacije, pojava znaka operacije posle operanada, ali, vidimo da je odsustvo zagrada, odnosno (praktičnije) - mogućnost izvršavanja operacija redom, bez 'dvoumljenja' - najvažnija odlika postfiksne notacije (isto važi i za prefiksnu notaciju, na koju ćemo se ukratko osvrnuti u sledećem odeljku).

** Algoritam po imenu Shunting Yard, koji se koristi za pretvaranje infiksnih izraza u postfiksne, 'najavili' smo u uvodnim poglavljima kao jedan od najvažnijih algoritama u računarskoj industriji (možda i najvažniji 🙂), i stoga ćemo na ovom mestu napraviti kratak osvrt na nekoliko važnih i zanimljivih osobina navedenog algoritma (pre svega, zarad nešto starijih i iskusnijih čitalaca, koji osećaju potrebu da se odmah malo više udube u tematiku članka):

pretvaranje infiksnog izraza u postfiksni, obavlja se u jednom prolasku kroz izraz
računanje vrednosti (postfiksnog) izraza, takođe se obavlja u jednom prolasku kroz izraz
ideja koja se koristi za pretvaranje infiksnih izraza u postfiksne, koristi se i za prevođenje programskog koda višeg nivoa (C, C++, Java, Python i sl) - u mašinski kod

Naravno, to su samo uvodne napomene, 'za sada' (detaljan opis postupaka za pretvaranje infiksnog izraza u postfiksni i računanje vrednosti izraza, prikazaćemo u zasebnim člancima, u bliskoj budućnosti).

Ukratko o prefiksnoj notaciji

Prefiksna notacija (nije teško pretpostaviti), podrazumeva sličan pristup kao i postfiksna notacija, s tom razlikom što se operator beleži pre operanada:

izraz a + b postaje +ab
izraz a + b * c postaje +a*bc

Procena vrednosti obavlja se 'u obrnutom smeru' u odnosu na idejno sličan postupak koji smo videli u prethodnom odeljku (npr. u drugom izrazu, prvo se obavlja množenje, pa onda sabiranje).

"Neobrnuta" poljska notacija takođe se koristi u računarskim algoritmima (bila je posebno popularna na prvim elektronskim kalkulatorima, pre više decenija), ali, za sada ćemo se zadržati na proučavanju i korišćenju postfiksne notacije, budući da takav zapis (ipak) prirodnije odgovara većini algoritama.

Uglavnom, u oba slučaja, oslobodili smo se zagrada (posle čega se vrednost izraza može izračunati u jednom prolasku), i samo još preostaje pitanje: kako od infiksnog izraza napraviti postfiksni.

Primer kreiranja postfiksnog izraza

Pre upoznavanja sa 'zvaničnim' postupkom za pretvaranje infiksnih izraza u postfiksne (što ostavljamo za drugu priliku), potrebno je da se upoznamo sa idejama koje stoje iza postupka - što ćemo najlakše izvesti ukoliko izraze predstavimo preko grafičkih simbola (ili, jednostavnije, preko "slika").

U izrazu prvo treba uočiti operaciju koja, u širem kontekstu, ima najniži prioritet (to jest, operaciju koja se izvršava 'na kraju'), i potom treba postaviti znak uočene operacije u koren "stabla" izraza (u konkretnom izrazu koji koristimo kao primer: a * (b + c), u pitanju je operacija množenja).

Ostali operatori iz izraza (tj. "znaci operacija"), raspoređuju se u stablo shodno prioritetu izvršavanja, što, u primeru koji koristimo, znači da će sa leve strane stajati promenljiva a (koja u množenju učestvuje samostalno), dok će sa desne strane biti "podstablo" * koje samo po sebi predstavlja operaciju sabiranja promenljivih b i c (operacija koja, očigledno, dolazi na red pre množenja zbira b + c sa promenljivom a).

Prebacivanje infiksne notacije u postfiksnu - Stablo — Slika 1. - Prebacivanje u postfiksni zapis - početna situacija - infiksni zapis predstavljen preko stabla.

Pošto je stablo formirano, pristupa se "obilasku stabla", na sledeći način: počevši od korena, na svakom čvoru koji predstavlja operaciju, prvo se "skreće" levo, a tek kada se dođe do 'krajnjeg levog čvora' (u bilo kom podstablu), sledi povratak jedan korak unazad - na čvor koji predstavlja operaciju - i potom se skreće desno, ali - posle svakog skretanja udesno (kada se nađemo u novom podstablu) - opet se prvo skreće levo (i opet se "držimo leve strane").

Kada se tokom kretanja kroz stablo pronađe operand (tj. promenljiva), odmah se prebacuje u postfiksni izraz, međutim, operatori (znaci operacija), mogu se prebacivati tek pošto je u postfiksni izraz već prebačeno celo podstablo koje je vezano za operaciju (tj, podstablo koje u korenu ima znak operacije).

U svemu (naravno) važi pravilo da se operand ili operator upisuje u postfiksni izraz samo jednom (prvi put kada dođe na red za upis).

Krenimo redom i pogledajmo postupak obilaska na primeru izraza koji smo do sada koristili: a * (b + c).

Prvo se u obzir uzima poslednja operacija koja se izvršava (znak množenja na vrhu stabla) ....

Prebacivanje infiksne notacije u postfiksnu - Korak 1 — Slika 2. - Prebacivanje u postfiksni zapis - korak 1(a).

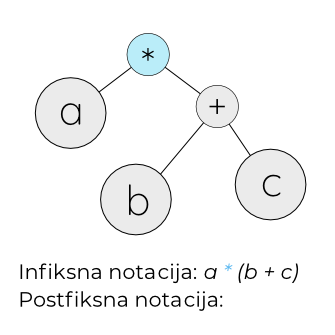
.... ali, pošto nijedan od znakova iz podstabala koja izviru iz korenog čvora, nije upisan, znak množenja se za sada mora preskočiti.

Prebacivanje infiksne notacije u postfiksnu - Korak 2 — Slika 3. - Prebacivanje u postfiksni zapis - korak 1(b) - operator se ne može upisati dok nisu upisana oba podstabla koja su povezana sa operatorom.

Prelazimo na levu stranu ....

Prebacivanje infiksne notacije u postfiksnu - Korak 3 — Slika 4. - Prebacivanje u postfiksni zapis - korak 2(a).

Čvor predstavlja promenljivu, i stoga će odmah biti prebačen u izraz sa postfiksnom notacijom.

Prebacivanje infiksne notacije u postfiksnu - Korak 4 — Slika 5. - Prebacivanje u postfiksni zapis - korak 2(b) - operand (a) može se upisati odmah (tj. bezuslovno).

Vraćamo se na prvi čvor ....

Prebacivanje infiksne notacije u postfiksnu - Korak 5 — Slika 6. - Prebacivanje u postfiksni zapis - korak 3(a).

.... ali, budući da ni sada nisu rešena oba podstabla korenog čvora (iako je leva strana rešena), čvor * se ni ovoga puta ne može prebaciti u izraz sa postfiksnom notacijom.

Prebacivanje infiksne notacije u postfiksnu - Korak 6 — Slika 7. - Prebacivanje u postfiksni zapis - korak 3(b) - Operator ne možemo upisati ni ovog puta.

Pošto u prethodnim koracima nismo završili u potpunosti sa prvim čvorom, ali, jesmo završili sa levim podstablom (čvor a), prelazimo na desno podstablo.

Usput ....

U pretposlednjem koraku rešili smo čvor a i odmah se vratili nazad na koreni čvor, zato što smo videli da čvor predstavlja operand - iz čega proizilazi da ne može imati podstabla.

U uobičajenom algoritamskom postupku (koji ćemo prikazati drugom prilikom), takođe se možemo osloniti na to da operand ne može biti koren (pod)stabla izraza, to jest, možemo se osloniti na to da posle operanda nema "daljeg grananja" (potrebno je samo da se operandi označe u programu na adekvatan način).

Međutim, u drugim stablima (kao što su npr. stabla pretrage), čvor sa brojčanom vrednošću može biti koren (pod)stabla, ali, u pitanju je sasvim drugačija struktura (čime ćemo se takođe baviti, ali, nekom drugom prilikom).

Vraćamo se na primer ....

U desnom podstablu, prvo se ispituje čvor koji odgovara operaciji sabiranja ....

Prebacivanje infiksne notacije u postfiksnu - Korak 7 — Slika 8. - Prebacivanje u postfiksni zapis - korak 4(a).

.... ali, budući da nijedno podstablo ovog čvora nije rešeno, za sada (u smislu ispisa), operator sabiranja se preskače.

Prebacivanje infiksne notacije u postfiksnu - Korak 8 — Slika 9. - Prebacivanje u postfiksni zapis - korak 4(b) - Operator se ne može upisati (nisu obiđena oba podstabla).

U korenu levog podstabla operacije sabiranja, nailazimo na operand b ....

Prebacivanje infiksne notacije u postfiksnu - Korak 9 — Slika 10. - Prebacivanje u postfiksni zapis - korak 5(a).

.... koji se odmah prebacuje u izraz sa postfiksnom notacijom.

Prebacivanje infiksne notacije u postfiksnu - Korak 10 — Slika 11. - Prebacivanje u postfiksni zapis - korak 5(b) - kao i u prethodnoj situaciji, operand se može upisati odmah.

Vraćamo se na operator sabiranja i ispitujemo da li je čvor + spreman za prebacivanje u postfiksni izraz ....

Prebacivanje infiksne notacije u postfiksnu - Korak 11 — Slika 12. - Prebacivanje u postfiksni zapis - korak 6(a).

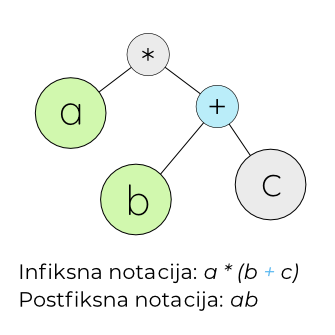
.... međutim, budući da desno podstablo operatora + nije rešeno, operator + se i dalje ne upisuje u postfiksni izraz.

Prebacivanje infiksne notacije u postfiksnu - Korak 12 — Slika 13. - Prebacivanje u postfiksni zapis - korak 6(b) - Operator + još uvek se ne sme upisivati.

Prelazimo u desno podstablo operacije sabiranja ....

Prebacivanje infiksne notacije u postfiksnu - Korak 13 — Slika 14. - Prebacivanje u postfiksni zapis - korak 7(a).

.... i odmah se operand c može prebaciti u izraz sa postfiksnom notacijom.

Prebacivanje infiksne notacije u postfiksnu - Korak 14 — Slika 15. - Prebacivanje u postfiksni zapis - korak 7(b) - Operand c može se upisati odmah.

Ponovo se vraćamo na čvor + ....

Prebacivanje infiksne notacije u postfiksnu - Korak 15 — Slika 16. - Prebacivanje u postfiksni zapis - korak 8(a).

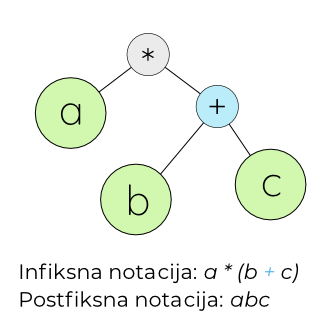
.... i sada se čvor + može prebaciti u izraz sa postfiksnom notacijom, budući da je rešeno celo podstablo koje se odnosi na operaciju sabiranja.

Prebacivanje infiksne notacije u postfiksnu - Korak 16 — Slika 17. - Prebacivanje u postfiksni zapis - korak 8(b) - Ovoga puta može se upisati operator (+).

Na kraju, vraćamo se na koreni čvor ....

Prebacivanje infiksne notacije u postfiksnu - Korak 17 — Slika 18. - Prebacivanje u postfiksni zapis - korak 9(a).

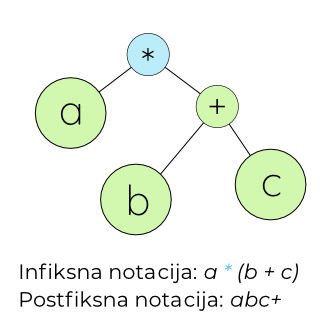
.... i budući da je celo stablo (osim korenog čvora), već prebačeno u izraz sa postfiksnom notacijom, može se upisati i sam koreni čvor.

Prebacivanje infiksne notacije u postfiksnu - Korak 18 — Slika 19. - Prebacivanje u postfiksni zapis - korak 9(b) - Na kraju, upisuje se i operator "*".

Cela operacija je završena: sve promenljive i svi znakovi operacija, prebačeni su u postfiksnu notaciju.

Prebacivanje infiksne notacije u postfiksnu - Korak 19 — Slika 20. - Prebacivanje u postfiksni zapis - Konačni rezultat.

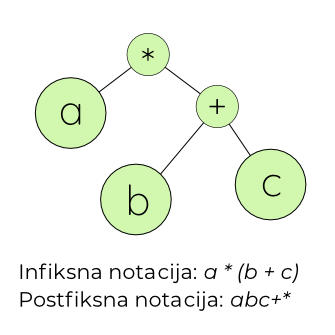
Ukoliko je potrebno, pogledajte ponovo ceo primer.

Prebacivanje infiksne notacije u postfiksnu - Animacija — Slika 21. - Prebacivanje u postfiksni zapis - Animacija.

Za vežbu ....

Na kraju, pokušajte sami da pretvorite bar nekoliko * infiksnih izraza u izraze sa postfiksnom notacijom - služeći se "papirom i olovkom".

Za proveru rezultata možete koristiti mini-aplikaciju ispod (dozvoljeni znaci: mala slova, znaci operacija i zagrade).

Postfiksna notacija:

--------

Za dalje istraživanje ....

Dodatne informacije u vezi sa različitim notacijama algebarskih izraza, možete pronaći preko sledećih linkova:

Prefiksna notacija Postfiksna notacija Jan Lukašijevič Edsger Dajkstra

Autor članka Nikola Vukićević Za web portal codeblog.rs

Napomena: Tekstovi, slike, web aplikacije i svi ostali sadržaji na sajtu codeblog.rs (osim u slučajevima gde je drugačije navedeno) predstavljaju intelektualnu svojinu autora sajta codeblog.rs i zabranjeno je njihovo korišćenje na drugim sajtovima i štampanim medijima, kao i bilo kakvo drugo korišćenje u komercijalne svrhe, bez eksplicitnog pismenog odobrenja autora.