Binarno stablo pretrage
Uvod
Binarno stablo pretrage je razgranata struktura podataka koja se u različitim računarskim sistemima koristi zarad efikasnog pretraživanja većih kolekcija podataka.
Stabla pretrage predstavljaju prilično značajnu pojavu (kako u obrazovnom tako i u praktičnom smislu), i stoga ćemo u bliskoj budućnosti započeti sa objavljivanjem članaka koji se tiču detaljnog opisa i implementacije jedne od mogućih struktura binarnog stabla pretrage (ima ih nekoliko), a u ovom članku - kako i dolikuje za sam početak - upoznaćemo se sa osnovnom strukturom stabala pretrage i (pre svega), sa opštim principima binarne pretrage.
Pošto prikažemo osnovnu strukturu stabla i pre nego što pređemo na diskusiju o upotrebi binarnih stabala, iskoristićemo priliku da se pozabavimo i drugim opštim pitanjima koja se tiču toga šta, u smislu brzine izvršavanja, možemo pri pisanju programa očekivati od računara i, što je važnije: šta, pri projektovanju programa, treba (kao programeri) - da očekujemo sami od sebe.
Osnovna struktura
Osnovni element strukture binarnog stabla je brojčani podatak koji se koristi kao jedinstveni ključ * pri obavljanju pretrage i prepoznaje se kao "čvor" (eng. node).
Svaki čvor povezan je sa okolnim čvorovima - sa najviše jednim čvorom sa prethodnog nivoa hijerarhije, i najviše dva čvora na sledećem nivou hijerarhije (npr. čvor #31 sa donje slike predstavlja jedinstveni celobrojni podatak, * 'predak' čvora #31 je čvor #12, a 'potomci' su čvorovi #20 i #43).
Naravno, u stablu postoji i jedan čvor bez pretka i (tipično), mnoštvo čvorova bez potomaka, a takvi čvorovi imaju i posebne nazive:
- 'čvor bez pretka' prepoznaje se kao "koreni čvor" (na slici, čvor #51)
- čvorovi bez potomaka (na slici, čvorovi #1, #11, #20, #43, #59, #71, #91 i #99), prepoznaju se kao "listovi"
Što se tiče rasporeda elemenata, za svaki čvor u stablu pretrage, ** važi sledeće pravilo: sve vrednosti u levom "podstablu" *** datog čvora, veće su od vrednosti koja je pripisana čvoru, a sve vrednosti u desnom podstablu, manje su od vrednosti koja je pripisana čvoru (npr. levo podstablo čvora #12 sadrži čvorove #1, #9 i #11, a desno podstablo, čvorove #20, #31 i #43).
Pretraga stabla i druge operacije, počinju od "korenog" čvora (tj. "korena stabla").
Sada, kada smo upoznati sa osnovnom ('geometrijskom') strukturom stabla pretrage, potrebno je da se upoznamo sa time kako se obavlja pretraga preko prikazane strukture, međutim, pre toga ćemo se 'vratiti na početak', tj. razmotrićemo opšte ideje koje prikazuju (pravu) upotrebnu vrednost stabala pretrage, kao i ideje koje se tiču neophodnosti korišćenja efikasnih algoritama ....
Malo istorije i "filozofije"
Pod uslovom da je na raspolaganju dovoljno procesorskih, memorijskih i ostalih kapaciteta, računarski sistemi omogućavaju smeštaj i obradu velikih količina podataka, velikom brzinom i (u najpraktičnijem smislu), svrha računara je da život ljudi učine lepšim, boljim i lakšim, pri čemu je obaveza programera - da udese da računari obavljaju zadatke kojima su namenjeni, na što jednostavniji način (to jest, što efikasnije).
Na početku, računari su imali veoma (!) skromne kapacitete i programeri su morali da se "dovijaju", "na sve moguće načine", da iz računara 'izvuku' što je moguće više (da ne kažemo - sa velikim uvažavanjem i simpatijama - da izvuku išta. :)), a danas, usled prilično vrtoglavog razvoja računarske industrije koji je za posledicu imao znatno uvećanje procesorskih i memorijskih kapaciteta u prvih pet decenija razvoja, prosečnom korisniku su stavljeni na raspolaganje računarski resursi o kakvima su programeri i korisnici pre 25 ili 30 godina mogli samo da maštaju (o prvim generacijama programera i korisnika, još 25 ili 30 godina unazad - da ne govorimo).
S obzirom na prethodno navedene smernice, neretko se dešava da se mlađi programeri zapitaju: koliko se u današnje vreme zapravo mora voditi računa o tome kakvi algoritmi se implementiraju pri rešavanju problema na računarima, ili (praktičnije), postavlja se pitanje: koliko se (zapravo) možemo osloniti na brzinu savremenih računara u izvršavanju programa?
Da pojasnimo ....
Većina programera uvažava to da razlike u efikasnosti različitih algoritama postoje (odnosno, to da su određeni algoritmi efikasniji od drugih), jasno je da su određeni algoritmi izrazito neefikasni sami po sebi (pa ih zato treba izbegavati), a takođe je krajnje jasno da realne performanse, čak i najefikasnijih algoritama, zavise od procesorske snage i memorijskih kapaciteta računara na kojima se programi izvršavaju.
Međutim, ako zanemarimo "očigledne" situacije (tj. "okršaje" između izrazito efikasnih i izrazito neefikasnih algoritama), i usmerimo se na mnoge uobičajene algoritme sa kakvima se susrećemo svakodnevno - i dalje se postavlja pitanje u vezi sa tim da li (u praktičnom smislu), postoji osetna razlika između vremena izvršavanja dva algoritma čije su klase vremenske složenosti približne?!
Da bismo što adekvatnije odgovorili na prethodno postavljena pitanja, prodiskutovaćemo ukratko o dva jednostavna algoritma za pretragu.
Pretraga nizova uopšteno
U računarskoj tehnici, statički niz, koji ćemo nazivati onako kako je uobičajeno - "niz", bez prefiksa (sve dok u budućim člancima ne dođemo do diskusije o strukturama podataka), može se posmatrati kao skup elemenata koji su u memoriji poređani jedan za drugim, tako da je svaki element, osim prvog i poslednjeg, * implicitno povezan sa tačno dva susedna elementa: sa elementom koji prethodi i elementom koji sledi.
Ukoliko je niz elemenata neuređen, na primer: 51, 9, 1, 20, 31, 43, 98, 59, 63, 99, 84, 91, 11, 71, 12, a naša je namera da ustanovimo da li se u datom nizu nalazi broj 71, program koji pretražuje niz, mora * - krenuvši od početka - ispitati svaki element niza, sve dok ne pronađe vrednost koju tražimo, ili - dok ne ustanovi da traženi broj ne postoji u nizu (u konkretnom primeru, broj 71 postoji u nizu i može se pronaći posle najviše 14 pokušaja).
S obzirom na male dimenzije niza koji smo koristili kao primer i budući da današnji računari jesu veoma brzi, traženi broj će biti pronađen u "deliću sekunde" (svakako nećemo svesno primetiti da je ikakvo vreme utrošeno na pretragu, i svakako - i dalje nismo ubeđeni da je postupak neefikasan).
Ukoliko se uzme da je vreme potrebno za obradu jednog elementa niza, jedan milioniti deo sekunde (tj. 1 mikrosekunda), vrednost 71 će u navedenim okolnostima biti pronađena za 14 mikrosekundi.
(U svakom slučaju, za sada sve deluje krajnje nezabrinjavajuće i, prosto rečeno - i dalje je u pitanju 'delić sekunde'.)
Nasuprot primerima malog obima, situacija se drastično menja ukoliko je potrebno pretraživati velike kolekcije (poslužićemo se primerom koji smo već nagovestili) ....
Uzmimo za primer pretragu baze podataka velike društvene mreže i situaciju u kojoj, broj koji se traži, predstavlja (jedinstveni) podatak preko koga se prepoznaje određeni korisnik mreže (odnosno, indeks preko koga se pristupa ostalim podacima o korisniku) i uzmimo da podaci u bazi nisu uređeni na optimalan način (u stvarnosti, gotovo je sigurno da programeri ne bi bili baš toliko "lenji", ali .... da ne kvarimo primer). :)
U svakom slučaju, u hipotetičkoj situaciji koju razmatramo, indeksi različitih korisnika su povezani jedan za drugim, i moraju se (i dalje) pretraživati redom.
Pretpostavićemo da baza podataka sadrži podatke za 250 miliona osoba (što je vrednost koja deluje "krupno", ali je takođe u pitanju prilično uobičajena vrednost u slučaju većih, popularnijih društvenih mreža, pri čemu najpopularnije društvene mreže često imaju još više korisnika), pa, ako pretpostavimo i to da je traženi broj (ponovo) pri kraju niza i da je za ispitivanje jednog sloga (ponovo) potreban jedan milioniti deo sekunde, neće biti teško da dođemo do zaključka da će računar (potencijalno, u najgorem slučaju), tražiti podatke o jednoj osobi preko četiri minuta (~250s = ~4 minuta i 10 sekundi) - što nikako nije prihvatljivo.
Kroz prethodni primer praktično smo pokazali zašto se - i dalje -- i te kako (!) -- mora voditi računa o racionalnom korišćenju računarskih resursa i takođe smo pokazali da računari nisu u stanju da obrađuju velike količine podataka velikom brzinom ukoliko se za obradu podataka ne koriste optimalni algoritmi.
U sledećem odeljku, pristupićemo pripremi strukture koja će omogućiti pretraživanje početne kolekcije podataka na (znatno) efikasniji način (vrednosti više neće biti povezane sa susednim vrednostima u rastućem (tj. neopadajućem) poretku, već - tako da tvore stablo pretrage (onako kako smo videli još na početku)).
Priprema strukture
U prethodnom odeljku koristili smo neuređen niz i 'usput se zapitali' da li bi (i u kojoj meri), uređen niz bio od pomoći.
Odgovor možemo dobiti ako prvobitni niz: 51, 9, 1, 20, 31, 43, 98, 59, 63, 99, 84, 91, 11, 71, 12, uredimo u neopadajući poredak: 1, 9, 11, 12, 20, 31, 43, 51, 59, 63, 71, 84, 91, 98, 99 - posle čega ćemo ponovo pokušati da pronađemo brojeve 71 i 12.
Broj 12 se ovoga puta može pronaći iz četiri pokušaja (što jeste dobro samo po sebi), ali zato pretraga broja 71 (koji je i dalje 'negde pri kraju') - i dalje podrazumeva prolazak kroz skoro ceo niz.
Shodno navedenom, nije teško doći do zaključka da uređenost niza u slučaju linearne pretrage - ne pomaže za prave, već pomaže samo u određenim okolnostima - onda kada se traže elementi koji su 'blizu početka' (dakle, u praktičnom smislu - 'nema boljitka').
Što se tiče (drugih) opštih uputstava, u praksi (zapravo) jeste potrebno da kolekcija podataka koja se pretražuje bude uređena, * ali - u svakom slučaju se mora osmisliti efikasniji postupak pretrage.
Jedno od mogućih rešenja, podrazumeva raspoređivanje elemenata niza u poredak binarnog stabla.
Kao što smo na samom početku naveli, u pitanju je razgranata struktura podataka koja se sastoji iz međusobno poveznanih "čvorova"), a pošto smo se već upoznali sa osnovnim 'tehničkim karakteristikama' binarnih stabala, svakako je red da se u nastavku upoznamo i sa opštim principima pretrage, tj. sa upotrebnom vrednošću strukture koju razmatramo.
Za primer ćemo uzeti uređenu * verziju niza koji smo do sada koristili kao primer, pri čemu se može primetiti da je u pitanju niz čiji se broj elemenata, n, u opštem smislu može izraziti kao 2h - 1 (u nastavku ćemo videti zašto smo baš na taj način formulisali broj elemenata).
Kao što smo naveli, opšti postupak za kreiranje binarnog stabla pretrage (koji je svakako ponešto kompleksniji od postupka koji sledi), biće tema detaljnog članaka o AVL stablima, međutim, uređeni niz koji vidimo na slici ispod, lako se može pretvoriti u kompletno balansirano binarno stablo pretrage - strukturu u kojoj je svaki pojedinačni podatak (tj. "čvor"), povezan sa 0 ili 2 susedna podatka (regularno binarno stablo - koje nije kompletno i balansirano - može imati i čvorove sa jednim "potomkom").
Za početak je potrebno izabrati središnji element niza za koren stabla (u našem slučaju, središnji element je broj 51).
U binarnom stablu pretrage (kao što smo ranije nagovestili), za svaki čvor važi sledeće pravilo: sve vrednosti koje se nalaze u podstablu sa leve strane posmatranog čvora, moraju biti manje od vrednosti koja je pripisana datom čvoru, dok se u desnom podstablu mogu naći samo vrednosti koje su veće.
Da bi navedeni uslov bio zadovoljen u slučaju stabla koje kreiramo * (preko niza koji je udešen tako da se od njega lako može napraviti kompletno binarno stablo pretrage), dovoljno je da u svakom koraku biramo 'sredine levih i desnih podnizova' i povezujemo ih sa čvorovima koji su već 'ubačeni' u stablo.
Da pojasnimo: u sledećem koraku, prepoznaćemo vrednosti na sredini levog i desnog odeljka prvobitnog niza (čvorovi #12 i #84) - i potom ćemo navedene čvorove povezati sa korenom stabla (čvor #51).
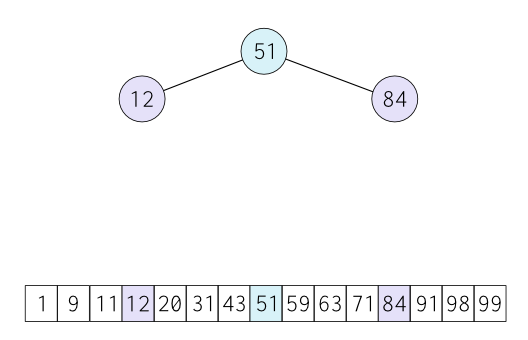
Potom se čvorovi #12 i #84 povezuju sa četiri čvora (#9, #31, #63, #98), koji predstavljaju sredine preostala četiri odeljka početnog niza ....
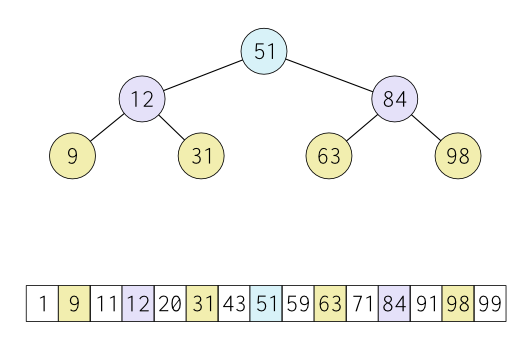
.... i, na kraju, preostali elementi (koji su, tehnički, takođe sredine preostalih "osmina" niza), takođe se povezuju sa stablom, po prethodno navedenim pravilima.
Binarno stablo je sada spremno za obavljanje pretrage.
Pretraga binarnog stabla
Vratićemo se na primer pronalaženja elementa sa vrednošću 71, ali - ovoga puta koristićemo stablo.
U prvom koraku, pristupa se korenom čvoru stabla, i proverava se da li koreni čvor sadrži traženu vrednost.
Budući da u prvom koraku nije pronađena vrednost 71 i budući da koreni čvor nije jedan od "listova" stabla, pretraga se nastavlja (da se podsetimo, list je element koji nema: ni levo, ni desno podstablo).
Broj koji je pripisan korenom čvoru (51), manji je od traženog broja (71), i stoga se, praktično, iz dalje pretrage može isključiti cela leva "polovina" stabla, * budući da je stablo formirano tako da su sve vrednosti u levom podstablu manje od vrednosti korenog čvora (51).
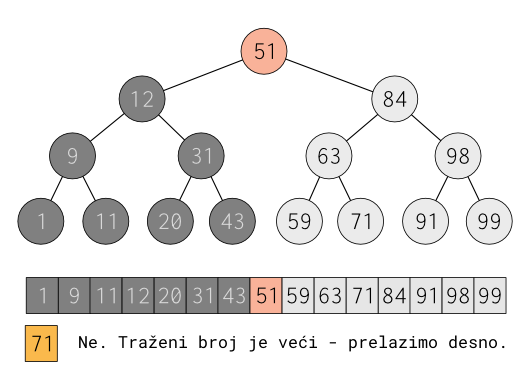
U sledećem koraku, ispituje se susedni desni čvor (koren desnog podstabla) ....
.... i budući da traženi broj nije pronađen, pretraga se nastavlja u levom podstablu čvora # 84 (s obzirom na to da je tražena vrednost, 71, manja od vrednosti čvora #84).
Pre prelaska na čvor #63, primetićemo da je na ovom mestu, takođe (efikasno - u jednom koraku), iz dalje pretrage isključeno celo desno podstablo čvora #84 (budući da navedeno podstablo sadrži isključivo vrednosti koje su veće od 84).
Vrednosti se ponovo porede ....
.... i budući da je tražena vrednost (71), veća od ispitivane vrednosti (63), pretraga prelazi na desno podstablo čvora #63, a levo podstablo isključuje se iz dalje pretrage.
Još jedno poređenje (na slikama se "vidi" da je u pitanju poslednje poređenje, ali, za računar je to samo "jedno od poređenja"):
Pogodak - traženi broj je pronađen.
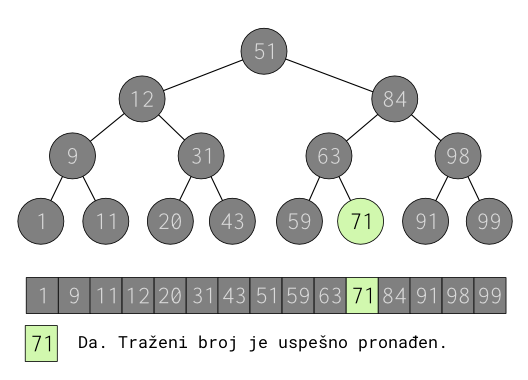
Tražena vrednost pronađena je iz svega četiri pokušaja!
Na početku smo naveli da se broj elemenata - n, izražava kao 2h - 1 i sada vidimo da je h, ništa drugo nego visina stabla (u ovom slučaju - 4 "sprata").
Kada bi se "listovi" (čvorovi #1, #11, #20, #43, #59, #71, #91 i #99), povezali sa po dva (nova) elementa, nastalo bi stablo visine 5 (u kome bi broj elemenata bio 31), a kada bismo postupak nastavili po istom principu, redom bi nastajale sledeće strukture stab(a)la:
- n = 63, h = 6;
- n = 127, h = 7;
- n = 255, h = 8
.... (preskačemo određeni raspon) ....
- n = 67108863, h = 27;
- n = 134217727, h = 28;
- n = 268435455, h = 29.
Iako se broj elemenata (približno) duplira u svakom koraku, visina raste za svega 1 "sprat", a budući da broj koraka u pronalaženju određenog elementa (u pravilno balansiranom stablu pretrage), zavisi isključivo od visine stabla (a ne od ukupnog broja elemenata), može se zaključiti da pronalaženje elementa u stablu pretrage koje povezuje preko 250 miliona elemenata, zahteva najviše 29 koraka.
Ako se setimo primera sa početka, i ponovo uzmemo 1 mikrosekundu kao vreme koje je potrebno da se pregleda jedan element stabla, može se zaključiti da pronalaženje određenog elemenata zahteva - u najgorem slučaju - 29 mikrosekundi, što je ogromna razlika (i ušteda) u odnosu na >4min (što je bio rezultat u slučaju linearne pretrage)!
Usput: da li ste - posmatrajući slike koje prikazuju pretragu binarnog stabla - obraćali pažnju na prikaz niza (u podnožju slike)?
Binarna pretraga uređenog niza
Pogledajte još jednom ceo postupak i ovoga puta (pogotovo ako u prvom "prolasku" niste obraćali pažnju na niz), posmatrajte i niz.
Uvidećete da se princip binarne pretrage može sprovesti u delo i nad običnim uređenim nizom, bez kreiranja stabla.
Međutim, stabla pretrage i te kako imaju važnu ulogu u u algoritmima, jer - u praksi - stabla se tipično ne koriste za pronalaženje samostalnih "brojeva", tj. indeksa, već (kao što smo ranije nagovestili), za pronalaženje kolekcija podataka koje su povezane sa indeksima.
Za sam kraj, mala rekapitulacija ....
.... a kada budete spremni i poželite da se detaljno upoznate sa visinski balansiranim (AVL) stablima, možete posetiti sledeći link: Visinski balansirana (AVL) stabla - članak.