Strukture podataka

Uvod

Za postizanje optimalnih rezultata u programiranju nije dovoljno samo da iza algoritama stoje optimalne ideje, već je takođe neophodno da sami podaci (nad kojima algoritmi operišu), budu formatirani na najefikasniji način (pogotovo kada su u pitanju velike kolekcije podataka).

U praktičnom smislu, termin 'struktura podataka' označava kolekciju međusobno povezanih podataka koji su u memoriji zapisani na način koji omogućava da se odgovori na prethodno postavljeni zahtev - pri čemu posebno važnu ulogu imaju relacije među podacima i operacije koje se tipično vezuju za određenu strukturu (umetanje elemenata u listu, pretraga u stablu, uklanjanje elementa sa steka i sl).

U apstraktnom smislu, termin 'struktura podataka' označava sam format koji se koristi za zapis.

Strukture podataka se najčešće implementiraju kao sistemi međusobno povezanih "čvorova" * (eng. node(s)), međutim, svakako su prisutni i drugi vidovi povezivanja.

Određene strukture podataka, kao što su statički nizovi, liste, stekovi, redovi za čekanje i stabla (o kojima govorimo u ovom tekstu i drugim člancima), dobro su poznate i često korišćene, i stoga je na početku ozbiljnijeg bavljenja programiranjem potrebno da se polaznici prvo upoznaju (upravo) sa navedenim strukturama. **

U dizajnu struktura podataka, važnu ulogu igraju pokazivači (posebne promenljive koje omogućavaju međusobno povezivanje podataka), i stoga je takođe neophodno da se u članku detaljno upoznamo i sa pokazivačima u programskom jeziku C (s tim da vredi napomenuti da je implementacija veoma slična i u drugim jezicima).

Klasifikacija struktura podataka

Za sam početak (zarad boljeg razumevanja), upoznaćemo se sa klasifikacijom struktura podataka preko nekoliko najvažnijih kriterijuma.

Podela struktura podataka prema topologiji

Shodno topologiji (odnosno tipu veza između podataka), strukture podataka mogu biti:

linearne
razgranate
umrežene

Linearne strukture podataka

Linearne strukture podataka su sastavljene od pojedinačnih podataka * koji su poređani jedan za drugim, bez grananja.

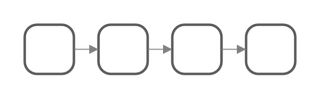
Primeri linearnih struktura podataka su: niz, lista, stek, red za čekanje.

Razgranate strukture podataka

Razgranate strukture podataka (tj. 'stabla'), odlikuju se hijerarhijskim rasporedom elemenata.

Bilo koji čvor (osim "korenog" čvora, koji se nalazi na vrhu hijerarhije i od koga počinju pretrage, obilasci i sl), povezan je sa:

tačno jednim čvorom sa prethodnog nivoa hijerarhije (čvor "predak")
proizvoljnim brojem čvorova sa sledećeg nivoa hijerarhije (čvorovi "potomci"/"deca")

Razgranate strukture podataka — Slika 2. - Opšta šema razgranate strukture podataka (podaci su poređani u obliku "stabla", što je istovremeno drugi, mnogo češće korišćen naziv za razgranate 'hijerarhijske' strukture).

U stablu obavezno postoje i čvorovi koji nemaju potomke (izraz za takav čvor je "list"), * a takođe je bitno pomenuti i to da nijedan čvor iz stabla ne sme pokazivati na čvorove iz susednih "podstabala" * (što je već implicirano kada je navedeno da bilo koji čvor može imati najviše jednog pretka). **

Umrežene strukture podataka

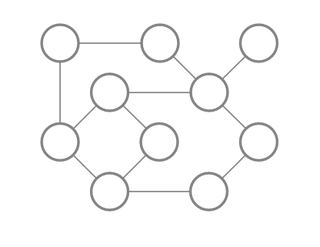
Umrežene strukture podataka (poznate i kao "grafovi"), sastoje se od čvorova koji su međusobno povezani na proizvoljan način.

Najjednostavnije: bilo koji čvor može biti povezan sa bilo kojim drugim čvorom, veze između čvorova ("ivice"), mogu biti jednosmerne i dvosmerne, i sl.

Podela struktura podataka prema mogućnosti dodavanja i uklanjanja elemenata

Prema mogućnosti dodavanja i uklanjanja pojedinačnih elemenata, strukture podataka se dele na:

statičke strukture podataka
dinamičke strukture podataka

Statičke strukture su strukture koje ne omogućavaju dodavanje i uklanjanje novih elemenata (npr. statički nizovi), dok su dinamičke strukture one koje omogućavaju dodavanje i uklanjanje elemenata (npr. lista, stek, red, stablo, graf i mnoge druge).

Na pojedinim mestima u literaturi, takođe se može naći dodatna podela dinamičkih struktura podataka, na strukture koje omogućavaju proizvoljno umetanje i uklanjanje elemenata (npr. liste), i strukture koje omogućavaju umetanje i uklanjanje elemenata samo pod određenim okolnostima, odnosno, na određenom mestu (npr. stek, red za čekanje).

Povezanost elemenata u statičkim strukturama podataka ostvaruje se implicitno (tj. posredno), time što susedni elementi zauzimaju susedne lokacije u računarskoj memoriji, dok se kod dinamičkih struktura podataka povezivanje vrši preko pokazivača (ili tzv. 'referenci', u zavisnosti od implementacije u konkretnom programskom jeziku).

Pokazivači

U članku o objektno orijentisanom programiranju mogli ste videti nekoliko primera koji prikazuju kako se više pojedinačnih podataka može 'spakovati' u jednu imenovanu celinu (tj. jedan "objekat"), pa samo još ostaje pitanje: kako omogućiti objektima da 'vide' jedni druge?

U praksi, rešenje je (kao što naslov poglavlja sugeriše), korišćenje pokazivača - promenljivih koje su u stanju da skladište memorijske adrese opšteg tipa i (što je za trenutnu diskusiju važnije) - adrese drugih promenljivih.

Pri definisanju klase koja predstavlja pojedinačni čvor, potrebno je (i dovoljno) da se među polja uvrsti i pokazivač koji će pokazivati na druge srodne objekte.

Pokazivači su u stanju da pokazuju na bilo koju memorijsku lokaciju (odnosno, u stanju su da čuvaju bilo koju adresu), ali, najčešće se koriste za skladištenje memorijskih adresa drugih promenljivih (bilo da su u pitanju osnovni podaci, slogovi ili objekti), i stoga su u mnogim jezicima uvedene tzv. reference - specijalizovani pokazivači koji mogu pokazivati samo na adrese drugih promenljivih.

U programskim jezicima C i C++, pokazivači se deklarišu uz navođenje znaka * ("zvezdica"), koji prethodi identifikatoru promenljive, a reference u C++-u se deklarišu navođenjem znaka & ("ampersend"), pre naziva promenljive.

		
int *p = &a; // pokazivač p (C/C++)
int &r = &a; // referenca r (C++)

Slika 4. - Opšti primer dodele adresa pokazivačima i referencama u programskom jeziku C/C++.

Vidimo na slici da pokazivač p pokazuje na adresu promenljive a (ili, jednostavnije, "pokazuje na promenljivu a"), to isto čini i referenca r, pri čemu se u oba slučaja adresa dobija preko operatora adresiranja & koji vraća adresu promenljive (u heksadekadnom formatu).

Kao što smo već naveli, pokazivač se može povezati i sa određenom memorijskom lokacijom 'opšteg tipa'.

Na primer:

			
void *p = (void*) 0x2400f0;

Slika 5. - Primer povezivanja pokazivača sa proizvoljnom memorijskom lokacijom;

Međutim, ovakav način upotrebe pokazivača nije od značaja za diskusiju o strukturama podataka (bar za sada 🙂).

Kada je potrebno zadati vrednost promenljivoj na koju pokazuje pokazivač ili referenca (ili kada je potrebno očitati vrednost), * važe sledeća pravila:

uz promenljivu koja predstavlja pokazivač, koristi se operator * (operator dereferenciranja)
uz reference se ne navodi dodatni operator

Na primer:

		
// 1. Deklaracija/inicijalizacija:
int *p = &a; // (C/C++)
int &r = &a; // (C++)

// 2. Zadavanje vrednosti:
*p = 12; // (C/C++)
r  = 12; // (C++)

// (Praktično: kao da smo naveli a = 12;)

// 3. Očitavanje vrednosti:
printf("a = %d\n", *p); // (C/C++)
printf("a = %d\n", r);  // (C++)

Slika 6. - Dodatni primeri upotrebe pokazivača i referenci u programskom jeziku C/C++.

Predavanje argumenata preko pokazivača ili referenci

Prodiskutovaćemo ukratko i o tome kako se ponašaju funkcije (tj. metode), u slučaju kada se parametri definišu preko pokazivača ili referenci, a kako u slučaju kada se parametri definišu kao podaci koji pripadaju nekom od osnovnih tipova (int, float char i sl).

Ukoliko se pri definisanju parametara funkcije ne koriste pokazivači (ili reference), osnovni tipovi podataka (char, int, float), predaju se po vrednosti, što zapravo znači da u telu funkcije nije moguće menjati vrednost promenljive koja je predata kao argument.

Na primer, pri pokretanju sledećeg programa:

		
#include<iostream>

using namespace std;

void promeni(int a) {
	a = a + 10;
}

int main() {
	int a = 5;
	promeni(a);
	std::cout << a;
}

Slika 7. - Primer pokretanja funkcije koja ne omogućava da se vrednosti argumenata menjaju (budući da parametri nisu definisani kao pokazivači ili reference).

.... ispis će biti "5" (budući da je funkciji promeni predata samo vrednost promenljive a iz funkcije main).

Ukoliko je (za razliku od prethodnog primera), parametar definisan kao pokazivač (ili referenca), pri pozivu funkcije dolazi do "predavanja (promenljive) po referenci":

		
#include<isotream>

using namespace std;

void promeni_pok(int *a) {
	*a = *a + 10;
}

void promeni_ref(int &a) {
	a = a + 10;
}

int main() {
	int a = 5;
	promeni_pok(&a);
	promeni_ref(&a);
	std::cout << a;
}

Slika 8. - Primer direktnog pristupa parametrima funkcije - preko pokazivača.

Ovoga puta ispis je "25", budući da su pokrenute obe funkcije, pri čemu svaka od dve funkcije praktično ima direktan pristup promenljivoj a iz funkcije main (i stoga se vrednost predatog argumenta dvaput uvećava za 10).

Da rezimiramo pravila ....

Ako se, pri definisanju (radne) funkcije, kao parametar navede promenljiva koja pripada nekom od osnovnih tipova podataka, * pri pozivu funkcije (u primeru: promeni(a);), dešava se sledeće: vrednost promenljive iz pozivajuće funkcije (u gornjem primeru, vrednost promenljive a iz funkcije main), kopira se i dodeljuje lokalnoj promenljivoj (parametar a iz funkcije promeni), ** ali - pošto je vrednost kopirana - prestaje bilo kakva povezanost između parametra tj. lokalne promenljive iz radne funkcije, i promenljive iz pozivajuće funkcije.

Nasuprot prethodnom slučaju: ako se, pri definisanju funkcije, kao parametar navede pokazivač ili referenca (u primerima koje smo prikazali, int* a i int& a), pri pozivu funkcije se ovoga puta predaje adresa promenljive iz pozivajuće funkcije, što znači da parametar radne funkcije (lokalna promenljiva), "pokazuje" na promenljivu iz pozivajuće funkcije, ili (malo drugačije), parametar radne funkcije povezuje se sa promenljivom iz pozivajuće funkcije (parametri int* a i int& a iz funkcija promeni_pok i promeni_ref, povezuju se sa promenljivom a iz funkcije main).

Ili, još jednostavnije: u najpraktičnijem smislu, radna funkcija direktno operiše nad promenljivom iz pozivajuće funkcije.

Sad je već vreme da se vratimo na glavne teme ....

Čvor (node)

U kontekstu diskusije o strukturama podataka, termin "čvor" označava kolekciju podataka koja sadrži jedan ili više podataka opšteg tipa, * i jedan ili više pokazivača na srodne čvorove.

Pojedinačni čvor se tipično implementira: ili kao slog (tj. struct), ili kao objekat klase, a bitno je navesti i to da čvorovi mogu (naravno) sadržati i pokazivače ili reference koji ne pokazuju na srodne čvorove, već pokazuju na druge podatke ('bilo kog' tipa).

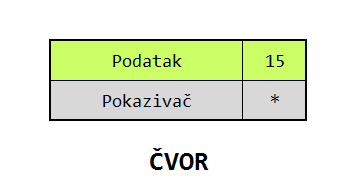
Na gornjoj slici je prikazana jednostavna struktura čvora koja se tipično sreće u ulančanim listama, a u donjem odeljku možemo videti i programski kod preko koga se prikazani čvor implementira.

		
struct Cvor {
	// Vrednost
	int v;

	// Pokazivač na sledeći čvor
	struct Cvor *sledeci;
};

Slika 10. - Primer definicije strukture čvora u programskom jeziku C/C++ (vrednost je zapisana preko celobrojne promenljive, a pokazivač je "u stanju" da pokazuje na "sledeći" čvor).

Dakle .... jedan čvor je u stanju da pamti adresu drugog (sličnog) čvora, drugi čvor (čija je adresa predata prvom čvoru), u stanju je da pamti adresu trećeg čvora, "treći čvor pamti četvrti" ..... što u praktičnom smislu znači da je moguće kreirati liste proizvoljne dužine.

Čak i najprostiji čvor koji smo videli nudi znatne mogućnosti kombinovanja, a za početak ćemo sagledati (u ovom članku), nekoliko najčešće korišćenih struktura podataka (koje smo naveli u uvodu), koje se mogu implementirati preko jednostavnih čvorova sa jednim podatkom i jednim pokazivačem.

U pitanju su sledeće strukture podataka:

ulančana lista (linked list)
magacin, odnosno stek (stack)
red za čekanje (queue)

Za binarna stabla je već potrebno implementirati čvorove sa dva pokazivača (što ćemo i prikazati nešto kasnije u članku), a stabla opšteg tipa se implementiraju preko čvorova sa listama pokazivača.

U ovom tekstu, na konkretne odlike navedenih struktura osvrnućemo se okvirno, međutim, zarad starijih/iskusnijih čitalaca * koje tematika struktura podataka zanima u većoj meri, spremili smo i zasebne, detaljne članke o većini struktura o kojima u članku pišemo (pojedinačni linkovi, u nastavku).

Kao svojevrstan uvod u glavnu temu članka, napravićemo osvrt na razlike između statičkih i dinamičkih nizova (jednostavan primer koji ilustruje upotrebnu vrednost struktura podataka koje nastaju povezivanjem čvorova).

Razlike između statičkih i dinamičkih nizova

Statički niz je najprostija struktura podataka koju smo u prethodnim člancima koristili, i do sada smo takvu strukturu jednostavno zvali - "niz".

Statički niz se implementira kao raspon susednih memorijskih lokacija koje se mogu rezervisati, i koristiti (u smislu pristupa i drugih operacija), kao svaka druga promenljiva, s tim da se niz u programskom kodu pojavljuje kao jedna imenovana promenljiva (sa više indeksa).

U pitanju je vrlo korisna struktura za smeštaj podataka (koja ima primenu u mnogim programima), pri čemu implementacija očigledno nije izvedena preko povezanih čvorova.

Struktura statičkog niza — Slika 11. - Statički niz čine susedne memorijske lokacije čiji je broj unapred definisan i ne može se menjati.

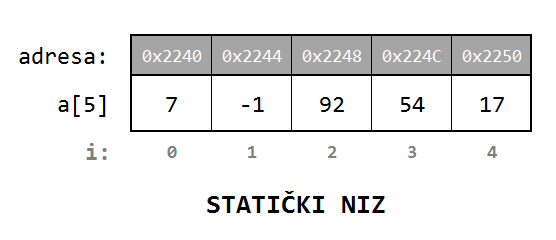
Osnovna prednost statičkih nizova u odnosu na liste (sa kojima ćemo se upoznati u ovom i narednom poglavlju), tiče se vremena pristupa određenom elementu (tj. "bilo kom elementu") - pri čemu vreme pristupa elementu ne zavisi od veličine niza (odnosno, od broja elemenata), međutim, statički niz (kao struktura podataka), ima i nekoliko očiglednih nedostatka:

maksimalni broj elemenata statičkog niza, praktično je ograničen na oko 500 hiljada *
veličina niza ne može se menjati naknadno

Problem ograničenosti kapaciteta statičkih nizova, tipično se rešava (kao što se da pretpostaviti :)), kreiranjem i upotrebom ulančanih lista.

U idejnom smislu, termin 'ulančana lista' (ili 'dinamički niz'), označava sistem u kome su čvorovi linearno poređani jedan za drugim, bez "grananja" i "petlji", ali, pošto u praksi nema 'obaveznog upisivanja u susedne memorijske lokacije', raspored čvorova u memoriji je nasumičan, tj. proizvoljan.

Svaki čvor pokazuje na jedan čvor (odnosno, na "sledeći" čvor), pri čemu je dozvoljeno proizvoljno (tj. "dinamičko") dodavanje, umetanje i uklanjanje čvorova * (ali, kao što smo već naglasili, nije dozvoljeno kreirati zatvorene 'petlje' u strukturi liste, niti hijerarhijske strukture koje su svojstvene stablima). **

Iako veličina dinamičkih nizova nije ograničena (makar teoretski), razume se da dinamički nizovi ne mogu imati doslovno neograničen broj elemenata (ne mogu zauzeti ni celokupan kapacitet RAM memorije, a kamoli zaista biti 'neograničeni'), međutim, povezivanjem čvorova mogu se kreirati liste koje su znatno veće od statičkih nizova. ***

* Dodavanje i umetanje su naizgled slični termini (koji se u literaturi koriste za obe operacije koje ćemo navesti), i najčešće se radi o sledećim vidovima upotrebe (koje smatramo najpravilnijim):

"dodavanje" je termin koji se (najčešće) odnosi na postavljanje novog elementa na kraj liste (tako da dotadašnji poslednji čvor pokazuje na novi čvor)
"umetanje" je termin koji se (gotovo uvek) odnosi na postavljanje novog čvora između dva proizvoljna čvora (tako da su čvorovi čija se veza raskida postavljanjem novog čvora, povezani preko novog čvora)

** Doduše, ukoliko koristimo elementarne čvorove sa jednim pokazivačem (kakve i koristimo), kreiranje hijerarhijske strukture nije ni izvodljivo. :)

*** Praktično: pre nego što deklarišemo statički niz od 100 hiljada elemenata, potrebno je da 'dobro razmislimo' o tome da li je takav niz neophodan.

Sa druge strane, kreiranje ulančanih lista sa više stotina hiljada elemenata (pa čak i milion ili više), sasvim je izvodljivo i prilično uobičajeno - pod uslovom da imamo na raspolaganju dovoljno RAM memorije.

Naravno, kreiranje velikih lista - osim što ima upotrebnu vrednost - takođe ima i "cenu".

Pristup elementu statičkog niza je algoritam složenosti O(1), dok je pristup elementu liste algoritam složenosti O(n).

U statičkom nizu, svejedno je da li se pristupa: prvom, trećem ili hiljaditom elementu; u listama (tj. 'dinamičkim nizovima') - nije, * a pored svega navedenog, u obzir treba uzeti i nezanemarljivo dodatno memorijsko zauzeće koje povlači upotreba pokazivača.

Međutim, 'nije sve tako crno' (ni iz daleka :)), to jest, problematici treba pristupiti na konstruktivan način.

Umesto da se opterećujemo nedostacima, koristićemo strukture podataka shodno njihovim 'dobrim stranama': *

statičke nizove najpraktičnije je koristiti za manje kolekcije podataka čija se veličina ne menja
liste se mogu koristiti za veće kolekcije podataka u kojima brza pretraga nije prioritet
za pretragu se (ionako) ne koriste liste, već, specijalizovana stabla ili hash mape

Ulančana lista (Linked List)

Pošto smo se upoznali sa opštim osobinama dinamičkih nizova, sledi kratko upoznavanje sa tri najuobičajenije implementacije dinamičkog niza (nakon čega sledi i kratko upoznavanje sa stablima).

Za početak ćemo napraviti dodatni osvrt na "jednostruko ulančane liste" - što predstavlja zvanični naziv za najosnovniju implementaciju dinamičkog niza (čiji je princip funkcionisanja opisan u prethodnom poglavlju, a opštu šema je prikazana na donjoj slici).

Slika 12. - Struktura čvorova ulančane liste: svaki čvor sastoji se od podatka i pokazivača (koji pokazuje na sledeći čvor). Pronalaženje elementa počinje od prvog čvora (pri čemu svaki čvor "zna" samo za susedni čvor); umetanje i uklanjanje čvorova su mogući na svim pozicijama.

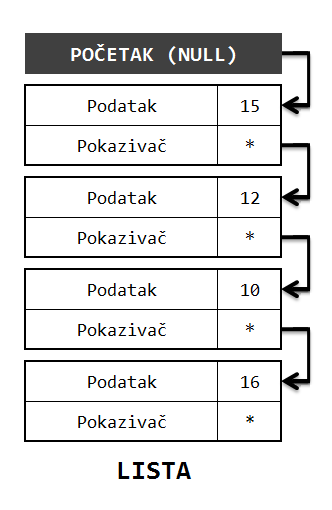
Kao što smo nagovestili u prethodnom poglavlju: * budući da pokazivač nekog čvora "zna" gde je sledeći element - bez obzira na to da li je sledeći element "odmah pored", "negde u blizini", ili je "daleko" - susedni čvorovi dinamičkih nizova ne moraju biti zapisani u susedne memorijske lokacije, već se mogu proizvoljno raspoređivati po slobodnim delovima memorije (za razliku od statičkih nizova gde je 'susednost elemenata' obavezna/zagarantovana i sl).

Drugim rečima, iako su u apstraktnom/idejnom smislu elementi ulančane liste poređani "jedan-za-drugim", konkretni podaci u računarskoj memoriji raspoređuju se 'onako kako je u datom trenutku najzgodnije'.

Kao što smo takođe naveli u prethodnim odeljcima, ulančane liste mogu se proširivati: dodavanjem čvorova na kraj, kao i proizvoljnim umetanjem elemenata na "međupozicije" (a moguće je naravno i uklanjati elemente).

Ako vas ulančane liste zanimaju u većoj meri, možete ispratiti link prema članku u kome je detaljno opisana implementacija jednostruko ulančane liste (u programskom jeziku C++), a u nastavku sledi opis dve strukture koje možemo smatrati "specijalnim varijacijama 'obične' ulančane liste".

Stek / magacin (stack)

Stek je linearna struktura podataka kod koje su pokazivači iskorišćeni tako da se može pristupati samo poslednjem ubačenom elementu, i u pitanju je (gotovo sigurno), najkorisnija jednostavna struktura podataka (mada ne i najzastupljenija; reklo bi se da ta "titula" ipak pripada ulančanim listama).

Da dodatno "potcrtamo poentu": za razliku od ulančanih lista, koje omogućavaju pristup proizvoljnom elementu, na steku se može pristupiti samo poslednjem dodatom čvoru (u cilju dodavanja novog čvora, zarad očitavanja vrednosti poslednjeg čvora ili zarad uklanjanja poslednjeg čvora).

Prethodno opisani princip uklanjanja elemenata sa steka (tj. u opštijem smislu, princip pristupanja elementima na steku), poznat je pod skraćenicom LIFO: "Last In - First Out".

Struktura čvorova steka — Slika 13. - Struktura steka: moguće je čitati samo poslednji ubačeni element, ili dodati novi element tako da "prekrije" element koji je do tada bio na vrhu steka.

Stekovi se koriste za praćenje pozicije u rekurzivnim pozivima, i takođe su neizostavan deo algoritama za prevođenje programskih jezika * kao i brojnih drugih algoritama.

Jednostavnu implementaciju steka za celobrojne vrednosti, ** možete videti u pretposlednjem poglavlju ovog članka.

Red za čekanje (Queue)

Red za čekanje je linearna struktura podataka kod koje su pokazivači iskorišćeni tako da se može pristupati samo prvom ubačenom elementu, i (slično kao stek), u pitanju je jednostavna linearna struktura od velike važnosti (koja se u programiranju koristi veoma često).

Da pojasnimo dodatno strukturu redova: za razliku od steka, u redovima za čekanje je moguće pristupiti samo prvom ubačenom elementu (zarad očitavanja vrednosti čvora ili zarad uklanjanja čvora), i pri tom se dodavanje elemenata obavlja na suprotnom kraju - preko zasebnog pokazivača.

Princip uklanjanja elementa iz reda za čekanje (tj. princip pristupanja elementima), poznat je pod skraćenicom FIFO ("First In - First Out").

Struktura čvorova reda za čekanje — Slika 14. - Struktura reda za čekanje (queue): dva zasebna pokazivača, jedan za čitanje (na kraju niza čvorova) i drugi za upis (na početku), omogućavaju upis novih elemenata i čitanje prvog ubačenog elementa (svi ostali elementi su nedostupni).

Po načinu funkcionisanja, redovi za čekanje u računarskim algoritmima, nalikuju redovima za čekanje koji se sreću u svakodnevnom životu (red na kasi u supermarketu, redovi na naplatnim rampama i sl).

Redovi za čekanje se takođe koriste u brojnim algoritmima (baš kao i stekovi), pri čemu ćemo pomenuti verovatno najpoznatiji primer upotrebe strukture reda za čekanje - algoritam BFS (u kome se red koristi za 'pamćenje' polja koja je potrebno obići nakon polja koje se trenutno obrađuje).

Stabla

Stablo je razgranata struktura podataka, tj. struktura koju karakteriše hijerarhijski raspored elemenata: "koreni čvor" sadrži dva ili više pokazivača, * pri čemu, nadalje, čvorovi "potomci" (na koje pokazuje koreni čvor), takođe imaju dva ili više pokazivača i pokazuju na svoje potomke ** ....

Da bismo detaljnije ilustrovali strukturu stabla, za primer ćemo uzeti binarna stabla, čiji su čvorovi sastavljeni od: podatka (ili podataka), i dva pokazivača (pokazivača koji pokazuje na levo podstablo i pokazivača koji pokazuje na desno podstablo).

Struktura čvorova binarnog stabla — Slika 15. - Struktura binarnog stabla: svaki čvor ima tačno dva pokazivača - jedan koji pokazuje na levi element (koji u stablima pretrage, po pripisanoj celobrojnoj vrednosti, mora biti manji), i jedan koji pokazuje na desni element (kome je u stablima pretrage pripisana veća celobrojna vrednost). Ukoliko je dati čvor "list" (čvor koji ne pokazuje na druge čvorove), pokazivači imaju vrednost NULL.

Čvorovi stabla ne mogu pokazivati na sopstvene pretke (ili proizvoljne čvorove iz susednih ili udaljenih podstabala), već samo mogu pokazivati na svoje direktne potomke (na čvorove koji su za jedan 'sprat' udaljeniji od korena u odnosu na posmatrani čvor, i ne pripadaju 'okolnim' podstablima).

Stabla imaju primenu u brzinskim pretragama različitih struktura podataka, i u prevođenju programskih jezika, a ako vas stabla zanimaju u većoj meri, Visinski balansiranim (AVL) stablima za pretragu i Binarnim stablima za predstavljanje algebarskih izraza, posvetili smo zasebne članke.

Praktičan primer: Implementacija steka u programskom jeziku C++

Za kraj, prikazaćemo jednostavnu (ali prilično kompletnu) implementaciju strukture steka, koja omogućava očitavanje vrednosti čvora, kao i umetanje i uklanjanje čvorova.

		
#include<iostream>
#include<stdlib.h>

struct Cvor {
	int         vrednost;
	struct Cvor *sledeci;  
};

class Stek {
public:

	struct Cvor *gornji;
	int brojac;

	Stek() {
		gornji = NULL;
		brojac = 0;
	}
	
	Stek(int v) {
		brojac = 0;
		push(v);
	}
	
	void push(int v) {
		// Prvo je potrebno kreirati novi čvor
		// (tj. potrebno je kreirati konkretan objekat
		// 'koji nije samo referenca'):

		struct Cvor *novi;
		novi = new Cvor();
		
		// Novom čvoru zadaje se uneta vrednost:

		novi->vrednost = v;
		
		// Novi čvor pokazivaće (u praktičnom smislu),
		// na dosadašnji "gornji element":
		
		novi->sledeci = gornji;
		
		// Pokazivač "Gornji" od sada
		// referencira novi čvor:
		
		gornji = novi;
		
		// Na kraju, ažurira se i
		// brojač čvorova:
		brojac++;
	}
	
	bool pop(int v) {
		// Ne smemo pokušavati da skinemo
		// čvor sa praznog steka!
		if (gornji == NULL) {
			return false;
		} else {
			// Bez pomoćnog čvora, dešava se sledeće:
			// -ako se prvo ukloni gornji čvor, izgubićemo
			// pokazivač na sledeći element ("donji",
			// "pretposlednji" element);
			// -ako se prvo premesti pokazivač "Gornji",
			// sa gornjeg čvora na pretposlednji,
			// izgubićemo pokazivač na gornji čvor -
			// koji je potrebno ukloniti preko
			// operatora delete (i stoga je jasno da je
			// pomoćni pokazivač - i te kako potreban).
			struct Cvor *c = gornji;
			gornji = gornji->sledeci;
			delete c;
		}

		return true;
	}
	
	int citanjeVrha() {
		return gornji->vrednost;
	}
};

int main() {
	struct Stek stek_1(10);
	
	std::cout << "Broj elemenata: ";
	std::cout << stek_1.brojac;
	std::cout << " Vrh steka: ";
	std::cout << stek_1.citanjeVrha() << std::endl;

	stek_1.push(12);
		
	std::cout << "Broj elemenata: ";
	std::cout << stek_1.brojac;
	std::cout << " Vrh steka: ";
	std::cout << stek_1.citanjeVrha() << std::endl;
}

Slika 16. - Primer implementacije steka preko klasa (u programskom jeziku C++).

Kao što vidimo, 'sve što treba' postiže se:

prostim dodelama vrednosti pokazivačima
upućivanjem pokazivača na drugu vrednost (koja može biti NULL ili adresa drugog čvora)
oslobađanjem memorije pri uklanjanju čvora. *

Takođe, stariji i iskusniji čitaoci mogu primetiti i sledeće: ako se pažljivije analizira prethodni programski kod, može delovati da je za implementaciju steka dovoljan samo slog Cvor (struct Cvor), odnosno, može delovati da se implementacija može izvesti bez upotrebe klase?!

Međutim, iako je navedeni pristup zanimljiv sam po sebi (i može biti korisna usputna vežba za studente I ili II godine fakulteta na kojima se izučava programiranje), u praksi, stavke kao što su preglednost koda i poštovanje opštih principa, imaju prioritet u odnosu na "lepe" i "akrobatske" kodove (odnosno: programiranje je aktivnost koja zahteva strateški pristup i vođenje računa o održivosti koda u daljoj eksploataciji).

Ako vam je potrebna dodatna ideja za vežbu, potrudite se da implementirate stek u programskom jeziku C (bez klasa, ali, uz uvažavanje opštih principa koje smo izneli u prethodnih nekoliko pasusa).

Autor članka Nikola Vukićević Za web portal codeblog.rs

Napomena: Tekstovi, slike, web aplikacije i svi ostali sadržaji na sajtu codeblog.rs (osim u slučajevima gde je drugačije navedeno) predstavljaju intelektualnu svojinu autora sajta codeblog.rs i zabranjeno je njihovo korišćenje na drugim sajtovima i štampanim medijima, kao i bilo kakvo drugo korišćenje u komercijalne svrhe, bez eksplicitnog pismenog odobrenja autora.