Uvod
Kada je u pitanju problematika obavljanja operacija sa "velikim" celobrojnim vrednostima na računaru, potrebno je prvo ustanoviti šta se (zapravo) smatra velikim brojevima u kontekstu diskusije koja je pred nama.
Recimo, 1000000 je svakako "veliki" broj (sam po sebi), ali - u pitanju je vrednost koja je višestruko manja od smeštajnog kapaciteta standardnih 32-bitnih (a pogotovo 64-bitnih) int registara na računarima.
Sa 32 bita, najveća apsolutna vrednost koja se može zapisati preko označene * promenljive, iznosi: 2147483647 (231 - 1), dok je najveća neoznačena vrednost: 4294967295 (232 - 1).
U slučaju da se koriste 64-bitne celobrojne promenljive - vrednosti su mnogo veće: 9223372036854775807 (263 - 1), odnosno 18446744073709551615 (264 - 1).
Dakle, veliki brojevi (u kontekstu ovog članka), su celobrojne vrednosti koje se ne mogu zapisati preko standardnih celobrojnih promenljivih, i stoga zahtevaju poseban postupak.
Da bismo mogli da operišemo nad zaista velikim brojevima, koji se ne mogu zapisivati neposredno (sa brojevima od 50, 100 ili više cifara) - predstavićemo brojeve kao nizove cifara.
Sabiranje velikih brojeva koji su predstavljeni kao nizovi cifara
Uzmimo za primer brojeve 1594 i 647 (čiji je zbir 2241).
Cifre dva navedena broja smestićemo u dva niza (a i b), i poravnati ih "uz desnu stranu", tako da se u oba slučaja cifra jedinica poklopi sa poslednjim elementom niza.
Kao što je poznato, cifra koja se pri sabiranju upisuje "ispod crte", dobija se sabiranjem svih cifara na datoj poziciji (u ovom slučaju, dve cifre), i 'prenosa', iz sabiranja sa prethodne (desne) pozicije, pri čemu se (iz ukupnog zbira) - za upis uzima cifra jedinica, a ostatak se prenosi u sledeću (levu) kolonu.
U primeru koji koristimo, prenos je cifra desetica (praktično, "leva cifra").
Ostaje samo pitanje: kako postupak sabiranja uobličiti algoritamski (tako da se može izvršavati na računaru).
Cifra koja se upisuje ispod crte, lako se dobija ispitivanjem ostatka pri celobrojnom deljenju sa 10, a cifra koja se prenosi u sledeću kolonu - deljenjem zbira sa 10.
Koristićemo sledeće formule:
cifra[i] = (a[i] + b[i] + prenos) % 10;
prenos = (a[i] + b[i] + prenos) / 10;
Prikazani postupak omogućava da se u potpunosti izbegnu grananja u programu - koja bi nastala ukoliko bismo ispitivali da li je zbir na datoj poziciji veći ili jednak deset!
Pored nizova a i b, za zapis ćemo koristiti i niz r (rezultat), kao i pomoćnu promenljivu p (prenos):
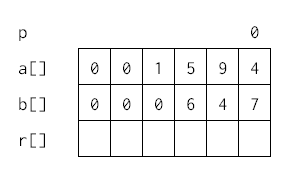
Pri računanju, krenućemo od poslednjeg mesta.
Zbir je 11, i stoga se cifra jedinica zapisuje u niz r, a cifra desetica zapisuje se kao ostatak (tj. 'prenos').

U sledećem koraku, zbir je 14 (cifra 4 se smešta u niz r, a cifra 1 se zapisuje kao prenos).
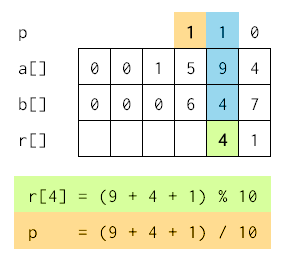
Postupak se ponavlja i u sledećoj koloni, rezultat je 12, što se raspoređuje na sledeći način: r[3] = 2; p = 1:

U poslednjem koraku rezultat je 2 (uz sledeću raspodelu: r[2] = 2; p = 0;):
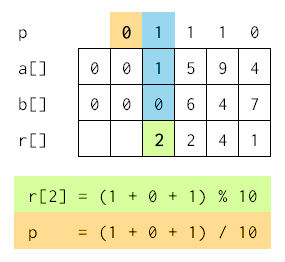
Pustićemo vas da sami "saberete nule" u poslednje dve kolone ....

.... pri čemu je rezultat koji se na kraju dobija, niz sa ciframa koje predstavljaju rezultat sabiranja: [0, 0, 2, 2, 4, 1].
Oduzimanje velikih brojeva koji su predstavljeni kao nizovi cifara
U prethodnom odeljku istakli smo da je jedna od najvažnijih odlika opisanog postupka sabiranja, to što je izbegnuto odlučivanje (odnosno grananje), čime su pojedinačni koraci svedeni na bezuslovno izvršavanje.
Potrebno je (naravno), da pojedinačni koraci u postupku oduzimanja - takođe budu svedeni na bezuslovno izvršavanje.
Rešenje je da se sve cifre iz "donjeg niza" oduzmu od broja 10 (što daje isti rezultat kao da se cifre iz "gornjeg niza" sabiraju sa brojem 10, samo što je preglednije) - nakon čega sledi sabiranje.
Međutim, ovoga puta (s obzirom na svojevrsnu pozajmicu koju pravimo), prenos će biti 0 - u slučaju da je zbir veći ili jednak 10, a u slučaju da je zbir manji, prenos će biti -1.
Ponovo ćemo za primer uzeti iste brojeve: 1594 i 647 (čija razlika je 947).
Niz koji predstavlja broj 1594 ostaće isti, dok će niz koji predstavlja broj 647, biti formiran tako što se svaka cifra oduzima od broja 10 (dosledno ćemo to uraditi čak i na pozicijama koje sadrže cifru 0), čime se dolazi do sledeće početne situacije.

Na poziciji cifre jedinica (počinjemo sa računanjem), sabiranjem cifara dobija se rezultat 7, i budući da je data vrednost manja od 10, prenos je -1.
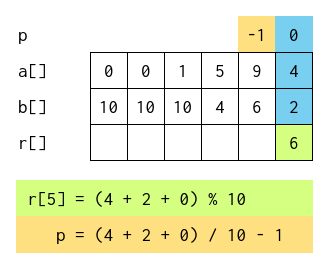
Sada, kada razumemo da metod 'funkcioniše', pogledajmo i implementaciju u C-u:
cifra[i] = (a[i] + b[i] + prenos) % 10;
prenos = (a[i] + b[i] + prenos) / 10 - 1;
Za prenos je samo potrebno oduzeti 1 od rezultata koji se dobija istim postupkom kao u slučaju sabiranja, jer sada (da se podsetimo), prenos treba da bude 0 kada je zbir cifara veći ili jednak deset (vrlo jednostavno i elegantno).
Pogledajmo računicu i na ostalim mestima.
U drugom koraku, izračunati zbir (14), veći je od 10, i stoga je prenos 0.
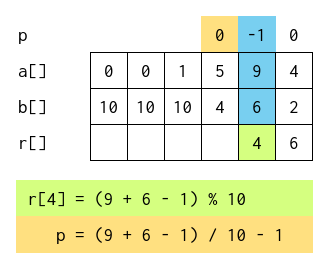
U trećem koraku, izračunati zbir (9), manji je od 10, i stoga je prenos -1.
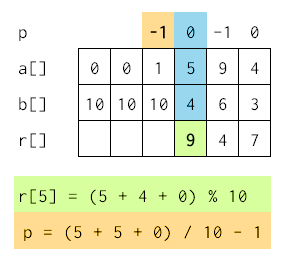
U četvrtom koraku, zbir je 10, a prenos 0.

U pretposlednjem koraku, zbir je (ponovo) 10 i prenos je (ponovo) 0 ....

.... kao i u poslednjem koraku:
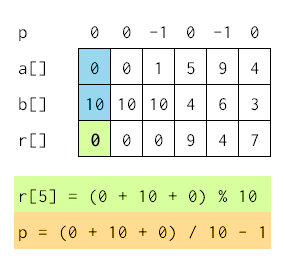
Dalje računanje se obustavlja, budući da smo došli do početka niza.

Rezultat je niz [0, 0, 0, 9, 4, 7] - baš kao što smo i očekivali.