Tutorijal - Prepoznavanje algebarskih izraza u tekstu
Uvod
U prošlom članku nagovestili smo da primena algoritma koji prepoznaje algebarske izraze predstavlja nepraktičan način za razvrstavanje algebarskih izraza i regularnih izraza (koji su zapisani preko regex literal sintakse u JavaScript-u), ali - sa druge strane - jasno je da su algoritmi za prepoznavanje algebarskih izraza prilično zanimljivi sami po sebi (i pri tom predstavljaju dobru vežbu za čitaoce koji u nekom trenutku planiraju da se upuste u samostalnu implementaciju prevodioca za određeni programski jezik).
U prepoznavanju algebarskih izraza (pri prevođenju programskih jezika), tipovi podataka igraju važnu ulogu. Na primer, u naredbi: a = b + c; - ukoliko promenljiva a nije brojčanog tipa - naredba se ne može izvršiti, a ako bilo koja od preostale dve promenljive takođe nije brojčanog tipa - izraz b + c ne može predstavljati algebarski izraz (već možda predstavlja naredbu za spajanje niski, ili (jednostavno), izraz koji ni u kom smislu nije pravilno formatiran). *
Međutim, u članku pred nama, nećemo se (ipak) baviti prevođenjem programskog koda u pravom smislu reči, smatraćemo da su promenljive uredno definisane, to jest, smatraćemo da izraz može biti algebarski izraz, a naš zadatak biće - da proverimo da li zaista jeste tako (što znači da se zapravo proverava: da li su tokeni sa desne strane naredbe dodele raspoređeni tako da tvore algebarski izraz).
Među tokenima ćemo lako prepoznati identifikatore i brojčane konstante, ali, na samom početku, najveći izazov će predstavljati prepoznavanje poziva funkcija. **
Prepoznavanje (poziva) funkcija u programskom kodu, odnosno - razlikovanje identifikatora funkcija od identifikatora promenljivih (tj. operanada), *** može delovati relativno komplikovano, međutim, uz dobro poznavanje algoritma Shunting Yard i malo promišljanja, zadatak postaje znatno lakši ....
Algoritam
Za razliku od prethodnog članka, u kome smo prvo razmatrali različite neefikasne algoritme (pre nego što smo se usmerili na efikasni postupak za prepoznavanje regularnih izraza), ovoga puta odmah ćemo se usmeriti na efikasni postupak (bez "rešavanja niza zagonetki od kojih je svaka komplikovanija od prethodne"), to jest, usmerićemo se na jedan od efikasnih postupaka.
U najprostijem smislu, ideja je sledeća: ako se određeni izraz (izdvojeni deo koda koji se proverava), posle pretvaranja u postfiksni oblik može interpretirati tako da se dobije korektan rezultat - može se smatrati da je izraz pravilno formatiran, to jest - može se smatrati da niz tokena predstavlja algebarski izraz.
Podsetimo se ukratko na drugu etapu algoritma Shunting Yard (na prvu etapu ćemo se podsetiti nešto kasnije).
Koristićemo kao primer postfiksni izraz ab- (koji je nastao prevođenjem infisknog izraza a - b), pri čemu će identifikatori a i b biti zamenjeni vrednostima promenljivih (smatraćemo da važi a = 2 i b =1):
Prva dva koraka podrazumevaju da se obe vrednosti smeste na stek (jedna za drugom) ....
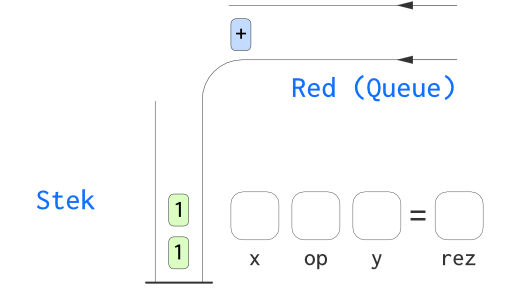
Pri pojavi operatora -, dva operanda sa vrha steka - uklanjaju se sa steka (i smeštaju se na pomoćne memorijske lokacije) ....
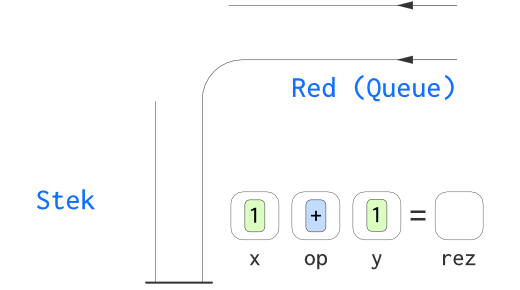
.... računa se vrednost izraza ....
.... i potom se izračunata vrednost vraća nazad na stek ....
Na kraju, pošto su potrošeni svi tokeni iz izraza, proverava se da li se na steku nalazi tačno jedan operand i, ako jeste tako (u primeru koji razmatramo, jeste) - izraz je pravilno formatiran, a vrednost izraza se nalazi na vrhu steka.
Međutim, bitno je primetiti sledeće: postupak je u idejnom smislu isti - bez obzira na tip operacije.
U bilo kom od četiri slučaja:
- sa vrha steka se preuzimaju dva operanda
- obavlja se operacija
- na stek se vraća jedan operand
Shodno navedenom, i budući da drugu etapu algoritma Shunting Yard koristimo samo da bismo ustanovili "da li se vrednost izraza može izračunati", a ne - da bi vrednost zapravo bila izračunata (to jest, budući da je samo potrebno ustanoviti da li je niz tokena poređan tako da tvori algebarski izraz) - u praktičnom smislu se može zanemariti sadržaj operanada i tip operacije - i potom se svi tokeni mogu svesti na jedan od dva moguća tokena:
- token "a" - koji predstavlja apstrakciju za (bilo koji/svaki) "operand"
- token "+" - koji predstavlja apstrakciju za (bilo koji/svaki) "operator"
Da ponovimo još jednom: u apstraktnom/opštem smislu (u situaciji kada je potrebno ustanoviti samo da li je izraz pravilno formatiran), bitno je samo da li - pri pojavi svakog operatora - sa steka mogu biti preuzeta dva operanda (posle čega se na stek "vraća" * samo jedan operand), i da li na kraju - pošto se postupak ponovi za sve operatore - na steku ostaje samo jedan operand.
Razmotrićemo i jedan konkretan primer.
Shodno svemu što smo naveli, sledeći infiksni izraz ....
(a + b) * c / (d - e)
.... može se prvo svesti na odgovarajući postfiksni oblik ....
ab+c*de-/
.... nakon čega se može svesti na 'apstraktni' oblik:
aa+a+aa++
Na kraju, 'apstraktni postfiksni izraz' se može svesti na jedan token "a" (u četiri koraka):
=> a a + a + a a + +
=> a a + a a + +
=> a a a + +
=> a a +
=> a
.... što ukazuje na to da je početni izraz (bio) pravilno formatiran.
Prepoznavanje različitih identifikatora u izrazu
Prethodna situacija u kojoj smo kao tokene koristili obične znakove (jedan znak - jedan token), bila je jednostavna za razmatranje, međutim, pravi izrazi su komplikovaniji:
let a = b1 * c1.v / (f1("+", d, e) + 19.58);
Prikazani izraz (koji ćemo koristiti kao novi primer), sam po sebi nije posebno zanimljiv, ali, sadrži sve elemente koje treba uzeti u obzir:
- identifikatore promenljivih -
b1 - objekte sa pripadajućim poljima -
c1.v - pozive funkcija -
f1("+", d, e) - brojčane konstante -
19.58
Pre svega, smatraćemo da su čitaoci (koje zanima tema članka), u stanju da iz cele naredbe izdvoje deo koji predstavlja izraz:
b * c1.v / (f1("+", c, d) + 19.58)
.... i da podele izraz na tokene.
Implementacija zavisi od toga da li (već) radite sa tokenima (ako je izraz prošao kroz lekser), ili ("baš") sa tekstom.
U drugom slučaju, regularni izraz koji traži razmake, tabove, znake operacija, zagrade i zareze, poslužiće sasvim dobro.
U svakom slučaju, "ulazna vrednost" (u nastavku, u glavnom algoritmu koji proučavamo), biće sledeća lista tokena:
/* ----- */
b
/* ----- */
*
/* ----- */
c1.v
/* ----- */
/
/* ----- */
(
/* ----- */
f1
/* ----- */
(
/* ----- */
"+"
/* ----- */
,
/* ----- */
c
/* ----- */
,
/* ----- */
d
/* ----- */
)
/* ----- */
+
/* ----- */
19.58
/* ----- */
)
/* ----- */
Identifikatori počinju znakovima abecede ili podvučenim crtama, a brojevi ciframa ili tačkom (po čemu ih možemo prepoznavati).
Ostali tokeni su samostalni.
Konačno, sve se svodi na pravilno tumačenje zagrada.
Razlikovanje zagrada koje pripadaju funkcijama od ostalih zagrada
U osnovnom tehničkom smislu (to jest, u smislu pojavnog oblika), token zagrade koja pripada funkciji (zagrada sa parametrima ili argumentima), nije naravno različit od tokena (slobodne) zagrade koja se inače koristi u izrazima, što znači da je glavni zadatak - ustanoviti kriterijum po kome se prepoznaje kontekst u kome se zagrade pojavljuju.
U prošlom članku, kada smo govorili o prepoznavanju regularnih izraza u naredbama, ustanovili smo da se regularni izrazi ne mogu pojavljivati posle identifikatora.
Ovoga puta situacija je "obrnuta": zagrade koje nas (više) zanimaju - one koje pripadaju funkcijama - pojavljuju se upravo posle identifikatora.
Pri interpretaciji izraza potrebno je voditi računa o tipu prethodnog tokena i - ako je pri pojavi otvorene zagrade prethodni token bio identifikator - može se smatrati da zagrada pripada funkciji, zbog čega treba 'podići' kontekst čitanja i zanemarivati sve tokene, sve dok se ne naiđe na odgovarajuću zatvorenu zagradu.
Preko navedenog postupka početni izraz se svodi na sledeći oblik:
b * c1.v / (f1 + 19.58)
Postupak kojim smo (ceo) poziv funkcije sveli na jedan token, može zbuniti neke od čitalaca (verujemo da je tako), i stoga ćemo dodatno pojasniti o čemu se radi.
U "pravom" algoritmu za računanje vrednosti izraza, pojava identifikatora promenljivih nije ništa drugo nego poziv da se vrednosti promenljivih pronađu i uvrste u izraz umesto identifikatora, kao na primer u sledećem izrazu, u kome poslednja naredba ....
let a = 10, b = 15, c;
c = a + b;
.... praktično postaje ....
c = 10 + 15;
Nije onda teško razumeti da poziv funkcije (u različitim izrazima), praktično pokreće izvršavanje funkcije, posle čega se pojava funkcije u izrazu - menja vrednošću, koja se dobija izvršavanjem funkcije.
Ako se privremeno usmerimo na drugi primer, možemo primetiti da poziv funkcije sabiranje u sledećem kodu ....
function sabiranje(a, b) {
return a + b;
}
let x = 10, y = 15;
let r = sabiranje(x, y);
.... praktično postaje ....
let r = sabiranje(10, 15)
.... odnosno, posle izvršavanja naredbe return a + b u funkciji sabiranje: *
let r = 25;
U apstraktnom smislu, izvršavanje funkcije f1 (u glavnom primeru koji koristimo u članku), može se svesti: prvo na identifikator f1, a zatim na token "a" (što je konvencija koju smo usvojili za označavanje "operanda ili vrednosti").
Pogledajmo kompletan primer koji ilustruje pretvaranje početnog izraza.
Primer tumačenja izraza
Pri tumačenju izraza, za početak se koristi prva etapa algoritma Shunting Yard (prebacivanje infiksne notacije u postfiksni oblik), što - kao što je poznato od ranije - podrazumeva upotrebu pomoćnog steka i reda (za čekanje) u koji se smeštaju obrađeni tokeni.
U izrazu koji razmatramo ....
b * c1.v / (f1("+", c, d) + 19.58)
.... prvi token (b) ....
b * c1.v / ( f1 ( \" + \" , c , d ) + 19.58 )
RED: [ ]
STEK: [ ]
KONTEKST: [ 0 ]
.... prepoznaje se kao operand i smešta se u red ....
* c1.v / ( f1 ( \" + \" , c , d ) + 19.58 )
RED: [ "b" ]
STEK: [ ]
KONTEKST: [ 0 ]
Drugi token (*), prepoznaje se kao operator i smešta se na stek ....
c1.v / ( f1 ( \" + \" , c , d ) + 19.58 )
RED: [ "b" ]
STEK: [ "*" ]
KONTEKST: [ 0 ]
Treći token unapred je prepoznat kao c1.v, ali, u red se prenosi (samo) "c1":
/ ( f1 ( \" + \" , c , d ) + 19.58 )
RED: [ "b" , "c1" ]
STEK: [ "*" ]
KONTEKST: [ 0 ]
Četvrti token / ima isti prioritet kao operator na vrhu steka (*), i stoga se prvo operator * premešta u red, a potom se operator / smešta na stek:
f1 ( \" + \" , c , d ) + 19.58 )
RED: [ "b" , "c1" , "*" ]
STEK: [ "/" ]
KONTEKST: [ 0 ]
Peti token (, prepoznaje se kao obična zagrada (zagradi prethodi operator), i stoga se zagrada direktno smešta na stek ....
f1 ( \" + \" , c , d ) + 19.58 )
RED: [ "b" , "c1" , "*" ]
STEK: [ "/" , "(" ]
KONTEKST: [ 0 ]
Šesti token (f1) prepoznaje se kao identifikator i smešta se u red.
( \" + \" , c , d ) + 19.58 )
RED: [ "b" , "c1" , "*" , "f1" ]
STEK: [ "/" , "(" ]
KONTEKST: [ 0 ]
Sedmi token ( - otvorena zagrada koja pripada funkciji (što algoritam prepoznaje po tome što zagradi prethodi identifikator, a ne operator) - sama po sebi se odbacuje, i takođe uvodi čitač u režim odbacivanja tokena (sve dok se ne pojavi odgovarajuća zatvorena zagrada) ....
\" + \" , c , d ) + 19.58 )
RED: [ "b" , "c1" , "*" , "f1" ]
STEK: [ "/" , "(" ]
KONTEKST: [ 0 , 3 ]
.... i stoga će tokeni: \", +, \", ,, c, ,, d i, na kraju, token ) - biti odbačeni, posle čega se kontekst vraća na 0 (usput, promenljiva kontekst je u funkcionalnom smislu takođe stek (kao i ranije), ali, ovoga puta smo joj dali drugi naziv da bismo je razlikovali od glavnog steka, koji koristimo za algoritam Shunting Yard) .
+ 19.58 )
RED: [ "b" , "c1" , "*" , "f1" ]
STEK: [ "/" , "(" ]
KONTEKST: [ 0 ]
Sledeći token (+) prepoznaje se kao operator i smešta se na stek.
19.58 )
RED: [ "b" , "c1" , "*" , "f1" ]
STEK: [ "/" , "(" , "+" ]
KONTEKST: [ 0 ]
Na kraju, token 19.58 se smešta u red ....
)
RED: [ "b" , "c1" , "*" , "f1" , "19.58" ]
STEK: [ "/" , "(" , "+" ]
KONTEKST: [ 0 ]
.... a token ) - zatvorena zagrada, povlači pražnjenje steka u red, sve do prve otvorene zagrade:
RED: [ "b" , "c1" , "*" , "f1" , "19.58" , "+" ]
STEK: [ "/" ]
KONTEKST: [ 0 ]
Budući da u izrazu nema više tokena (zatvorena zagrada je ujedno bila i poslednji token u izrazu), pravila nalažu da se tokeni * iz steka premeste u red (jedan po jedan):
RED: [ "b" , "c1" , "*" , "f1" , "19.58" , "+" , "/" ]
STEK: [ ]
KONTEKST: [ 0 ]
Red je formiran, i može se pristupiti tumačenju izraza. **
Tumačenje postfiksnog izraza
Za tumačenje izraza, koristićemo drugu etapu algoritma Shunting Yard.
Prema konvencijama koje smo utvrdili na početku, tokene početnog izraza (koji su smešteni u red za čekanje) ....
RED: [ "b" , "c1" , "*" , "f1" , "19.58" , "+" , "/" ]
STEK: [ ]
.... prvo treba svesti na apstraktni oblik:
RED: [ "a" , "a" , "+", "a" , "a" , "+" , "+" ]
STEK: [ ]
Budući da je sve spremno, može se započeti sa tumačenjem izraza.
Sve do pojave operatora, tokeni iz reda se prebacuju na stek (jedan za drugim).
RED: [ "+", "a" , "a" , "+" , "+" ]
STEK: [ "a" , "a" ]
Kao što znamo od ranije, pojava operatora, povlači preuzimanje dva operanda sa steka ....
RED: [ "a" , "a" , "+" , "+" ]
STEK: [ ]
OP1: "a"
OP2: "a"
.... nakon čega se obavlja operacija, a rezultat se vraća na stek.
Međutim, u praktičnom smislu, budući da se sa steka preuzimaju dva tokena "a" i vraća jedan, u implementaciji je dovoljno proveriti da li na steku postoje (bar) dva operanda i - ako je navedeni uslov zadovoljen - jednostavno sa steka treba ukloniti jedan operand (2 - 1 = 1).
RED: [ "a" , "a" , "+" , "+" ]
STEK: [ "a" ]
U nastavku, ponovo se operandi sa leve strane reda 'slivaju' na stek ....
RED: [ "+" , "+" ]
STEK: [ "a" , "a" , "a" ]
.... nakon čega ponovo sledi računanje:
RED: [ "+" ]
STEK: [ "a" ]
OP1: "a"
OP2: "a"
Drugi operator takođe nailazi na dva operanda na steku, i potom se obavlja "računanje" a rezultat se "vraća" na stek (ali, prema ranijem 'dogovoru', zapravo nema "računanja" i skripta će jednostavno ukloniti jedan operand sa steka) ....
RED: [ "+" ]
STEK: [ "a" , "a" ]
Na kraju, ceo postupak se ponavlja još jednom:
RED: [ ]
STEK: [ "a" ]
Budući da su tokeni iz izraza (tj. iz reda za čekanje), potrošeni, i budući da se na steku nalazi tačno jedan operand (koji bi inače bio rezultat računanja) - može se zaključiti da je izraz pravilno interpretiran, to jest - može se zaključiti da je uspešno prepoznat algebarski izraz.
Ideje za dalje unapređenje
U članku smo "pretresli" dobar deo onoga što je potrebno obaviti, ali - ne i sve (jednostavno rečeno, želimo da potaknemo čitaoce da samostalno istražuju određene delove implementacije).
U kontekstu mogućih unapređenja, pomenućemo dve ideje:
- prepoznavanje kompleksnijih operatora (
++,/=i sl) - prepoznavanje brojčanih konstanti (ideja koju smo još ranije nagovestili)
Kao što rekosmo, nećemo otkrivati baš sve i ostavićemo vas da sami smislite postupak za prepoznavanje operatora koji se zapisuju uz upotrebu dva znaka (ili više znakova), kao i postupak za prepoznavanje brojčanih konstanti.
U svemu navedenom, razmislite o sledećem:
- postoji li suštinska razlika u tumačenju unarnih i binarnih operatora (u smislu interakcije sa operandima)?
- da li (možda) pravila za definisanje identifikatora promenljivih pomažu u prepoznavanju brojčanih konstanti? *
Na kraju, postavlja se i pitanje - kako prepoznavati ternarni operator ? (možda smo mi "zaboravili" na ternarni operator, ali, "ternarni operator nije zaboravio nas").
Zanimljive teme za razmišljanje i razradu.
Za kraj ....
Ovim člankom zaključujemo mini-serijal o obradi teksta (odnosno, obradi programskog koda), koji smo pokrenuli člankom o samostalnoj implementaciji skripte za označavanje sintaksnih elemenata.
Ako želite da dalje istražujete oblast tumačenja programskog koda, samostalna izrada parsera je i dalje osnovna ideja koju vredi pratiti.
Kao što smo već pominjali, projektovanje i implementacija parsera svakako nije "lagan" projekat, pogotovo ne za početnike (pri čemu, ovoga puta, pojam "početnik" vezujemo za nekoga ko do sada nije pisao programe kakve prikazujemo u članku, a ne za nekoga ko doslovno tek počinje da se bavi programiranjem).
Međutim, projekat nije ni "najteži mogući" (ni iz daleka), pa - ako imate dovoljno slobodnog vremena i dobre volje :) ....